题目内容
9. 一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
分析 方法一:观察数表,可以发现规律:每一行都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第99行公差为297,第100行(最后一行)只有一个数,得出结果;
方法二;从第一行为1,2,3 和1,2,3,4,5的两个“小三角形”的例子,结合选项归纳得出结果,猜测出该数表的最后一行的数
解答 解:方法一:数表的每一行都是等差数列,且第一行公差为1,第二行公差为2,第三行公差为4,…,第99行公差为297,最后一行的数=(1+100)×298=101×298;
方法二:从第一行为1,2,3 及1,2,3,4,5的两个“小三角形”的例子,可归纳出结果为(3+1)×21及(5+1)×23,从而猜测最后一行的数为(100+1)×2100-2=101×298;
故答案为:101×298.
点评 本题考查了由数表探究数列规律的问题,解答这类问题时,可以由简单的例子观察分析,总结规律,得出结论.

练习册系列答案
相关题目
14.已知函数f(x)(x∈R)是偶函数,函数f(x-2)是奇函数,且f(1)=1,则f(2015)=( )
| A. | 2015 | B. | -2015 | C. | 1 | D. | -1 |
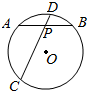 如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.
如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.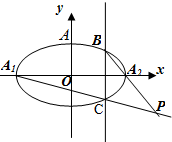 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.