题目内容
10．已知函数f（x）=$\frac{alnx+b}{{e}^{x}}$（e是自然对数的底数，其中常数a，n满足a＞b，且a+b=1，函数y=f（x）的图象在点（1，f（1））处的切线斜率是2-$\frac{1}{a}$．（Ⅰ）求a，b的值；
（Ⅱ）求函数f（x）的单调区间．
分析 （Ⅰ）求出函数的导数，由条件可得a，b的方程，解方程可得a=e，b=1-e；
（Ⅱ）求出f（x）的导数，由x=e，求得导数，再由x＞e，结合对数的性质可得减区间，由0＜x＜e可得增区间．
解答 解：（Ⅰ）f（x）=$\frac{alnx+b}{{e}^{x}}$的导数为f′（x）=$\frac{a-bx-axlnx}{x{e}^{x}}$（x＞0），
由f′（1）=2-$\frac{1}{a}$，得$\frac{a-b}{e}$=2-$\frac{1}{a}$，由a+b=1，可得$\frac{2a-1}{e}$=2-$\frac{1}{a}$，
即$\frac{2a-1}{e}$=$\frac{2a-1}{a}$，由a＞b，a$≠\frac{1}{2}$，则a=e，b=1-e；
（Ⅱ）由（Ⅰ）可得f′（x）=$\frac{e+（e-1）x-exlnx}{x{e}^{x}}$（x＞0），
即f′（x）=$\frac{e-x+ex（1-lnx）}{x{e}^{x}}$（x＞0），
由x=e时，f′（e）=0，且x＞e，e-x＞0，ex（1-lnx）＜0，
故f′（x）＜0，同理0＜x＜e，f′（x）＞0，
于是函数的单调增区间为（0，e），减区间为（e，+∞）．
点评 本题考查导数的运用：求切线方程和单调区间，主要考查导数的几何意义，正确求导和运用函数的性质是解题的关键，属于中档题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
5．$\frac{\frac{1}{2}-si{n}^{2}25°}{cos20°•cos70°}$=（ ）
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，则A=2，ω=2，F（$\frac{π}{3}$）=1．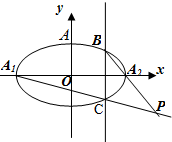
如图已知椭圆G：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右两个焦点分别为F1、F2，设A（0，b），若△AF1F2为正三角形且周长为6．