题目内容
5. 将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )
将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )| A. | 4 | B. | B6 | C. | $\frac{25}{4}$ | D. | $\frac{13}{2}$ |
分析 仔细阅读题意得出:每一横行上的数据的和也为等差数列,
利用每一横行上的数据为等差数列,得出第一行a1=$\frac{5}{2}$(D+A),第四行a4=$\frac{5}{2}$(B+C),
考虑等差数列的求和性质的a1+a2+a3+a4=$\frac{5}{2}$(a1+a4)=$\frac{25}{4}$(A+B+C+D),整体求解即可.
解答 解:根据题意可判断:使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,
所以每一横行上的数据的和也为等差数列,
设{an}为第n横行上的数据的和,
∴a1=$\frac{5}{2}$(D+A),a4=$\frac{5}{2}$(B+C),
∴a1+a2+a3+a4=$\frac{5}{2}$(a1+a4)=$\frac{25}{4}$(A+B+C+D),
∵A,B,C,D处的四个数互不相同且和为1,
∴$\frac{25}{4}$×1=$\frac{25}{4}$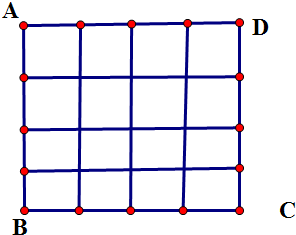
故选:C
点评 本题考查了数列在实际问题中的应用,结合图形判断,形象直观,整体运用等差数列的性质求解,考查了学生的分析解决问题的能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
15.$\frac{3+2i}{2-3i}$( )
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
16.已知命题p:sinα-cosα=$\sqrt{2}$,命题q:双曲线$\frac{{x}^{2}}{co{s}^{2}α}$-$\frac{{y}^{2}}{si{n}^{2}α}$=1的渐近线与圆x2+(y-1)2=$\frac{1}{2}$相切,则命题p为命题q为( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知函数f(x)=|2x+1|+|2x-3|,若关于x的不等式f(x)<|a-1|的解集非空,则实数a的取值范围是( )
| A. | [-3,5] | B. | (-3,5) | C. | (-∞,-3]∪[5,+∞) | D. | (-∞,-3)∪(5,+∞) |
20.已知底面边长为$\sqrt{3}$的正三棱柱ABC-A1B1C1的体积为$\frac{9}{4}$,若点P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
15.若x∈[0,2π],则sinx+cosx<1的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.
对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.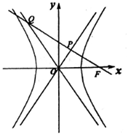 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.