题目内容
已知集合P={x|x2-8x-20≤0},S={x||x-1|≤m}.
(1)若(P∪S)⊆P,求实数m的取值范围;
(2)是否存在实数m,使得“x∈P”是“x∈S”的充要条件?若存在,求出m的取值范围;若不存在,请说明理由.
(1)若(P∪S)⊆P,求实数m的取值范围;
(2)是否存在实数m,使得“x∈P”是“x∈S”的充要条件?若存在,求出m的取值范围;若不存在,请说明理由.
(1)(-∞,3] (2)不存在,见解析
解:由x2-8x-20≤0解得-2≤x≤10,∴P={x|-2≤x≤10}.
由|x-1|≤m可得1-m≤x≤1+m,∴S={x|1-m≤x≤1+m}.
(1)要使(P∪S)⊆P,则S⊆P,
①若S=∅,此时,m<0.
②若S≠∅,此时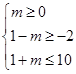 ,解得0≤m≤3.
,解得0≤m≤3.
综合①②知实数m的取值范围为(-∞,3].
(2)由题意“x∈P”是“x∈S”的充要条件,则S=P,
则 ∴
∴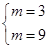
∴这样的m不存在.
由|x-1|≤m可得1-m≤x≤1+m,∴S={x|1-m≤x≤1+m}.
(1)要使(P∪S)⊆P,则S⊆P,
①若S=∅,此时,m<0.
②若S≠∅,此时
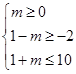 ,解得0≤m≤3.
,解得0≤m≤3.综合①②知实数m的取值范围为(-∞,3].
(2)由题意“x∈P”是“x∈S”的充要条件,则S=P,
则
 ∴
∴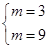
∴这样的m不存在.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 ,则”
,则” 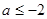 ”是”
”是” 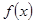 在R上单调递减”的( )
在R上单调递减”的( )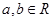 ,则“
,则“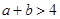 ”是“
”是“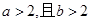 ”的( )
”的( )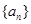 是公比为
是公比为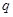 的等比数列,则“
的等比数列,则“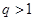 ”是“
”是“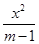 +
+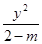 =1表示的焦点在y轴上的椭圆,且p是q的充分不必要条件,a的取值范围为________.
=1表示的焦点在y轴上的椭圆,且p是q的充分不必要条件,a的取值范围为________.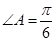 ”是“
”是“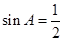 ”的( )
”的( ) 的充要条件
的充要条件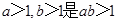 的充分条件
的充分条件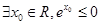
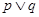 为真命题,则
为真命题,则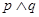 为真
为真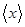 表示不小于x的最小整数,例如
表示不小于x的最小整数,例如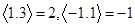 ,那么“
,那么“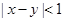 ”是“
”是“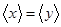 ”的( )
”的( )