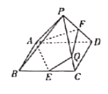
题目内容
【题目】已知三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,设点
,设点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,通过证
,通过证![]() ,并说明
,并说明![]() 平面
平面![]() ,来证明
,来证明![]() 平面
平面![]()
(2)采用建系法以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别表示出对应的点
,分别表示出对应的点![]() 坐标,设平面
坐标,设平面![]() 的一个法向量为
的一个法向量为![]() ,结合直线对应的
,结合直线对应的![]() 和法向量
和法向量![]() ,利用向量夹角的余弦公式进行求解即可
,利用向量夹角的余弦公式进行求解即可
![]() 证明:如图,
证明:如图,
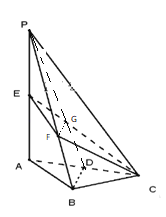
连接![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,
,![]() 点
点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
![]() 点
点![]() 为
为![]() 的重心,则
的重心,则![]() ,
,![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,可得
,可得![]() ,又
,又![]() ,
,
则以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
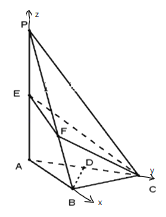
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由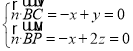 ,
,
取![]() ,得
,得![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() .
.![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.