Question

【题目】如图，点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为（ ）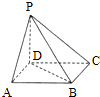
A.30°
B.45°
C.60°
D.90°

Answer 1

【答案】C
【解析】解：如图，以D为坐标原点，DA所在直线为x轴，DC所在线为y轴，DP所在线为z轴，建立空间坐标系， ∵点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，令PD=AD=1
∴A（1，0，0），P（0，0，1），B（1，1，0），D（0，0，0）
∴ =（1，0，﹣1）， =（﹣1，﹣1，0）
∴cosθ= =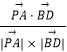
故两向量夹角的余弦值为 ，即两直线PA与BD所成角的度数为60°．
故选C
本题求解宜用向量法来做，以D为坐标原点，建立空间坐标系，求出两直线的方向向量，利用数量积公式求夹角即可