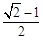题目内容
设P是双曲线 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
| A.4 | B.5 | C.6 | D.7 |
D
解析试题分析:由双曲线焦点三角形面积公式得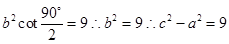 ,
,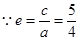
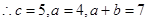
考点:双曲线方程及性质
点评:双曲线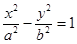 上一点P,则焦点三角形
上一点P,则焦点三角形 面积为
面积为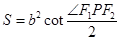

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知 是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引
是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引 的平分线的垂线,垂足为P,则点P的轨迹是
的平分线的垂线,垂足为P,则点P的轨迹是
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
方程mx2-my2=n中,若mn<0,则方程的曲线是( )
| A.焦点在x轴上的椭圆 | B.焦点在x轴上的双曲线 |
| C.焦点在y轴上的椭圆 | D.焦点在y轴上的双曲线 |
以双曲线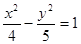 的离心率为首项,以函数
的离心率为首项,以函数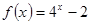 的零点为公比的等比数列的前
的零点为公比的等比数列的前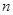 项的和
项的和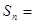
A.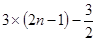 | B.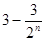 | C.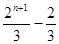 | D.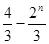 |
双曲线 =1的焦点到渐近线的距离为( )。
=1的焦点到渐近线的距离为( )。
A.2 | B.2 | C. | D.1 |

 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为 ),交
),交 轴于点
轴于点 .若
.若 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为


 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过点
的左、右焦点,过点 为直径的圆外,则双曲线离心率的取值范围是
为直径的圆外,则双曲线离心率的取值范围是



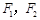 ,过
,过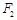 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点 ,
, 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )