题目内容
设椭圆的两个焦点分别为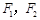 ,过
,过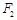 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点 ,
,
若 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )
A. | B.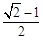 | C. | D. |
D
解析试题分析:解:设点P在x轴上方,坐标为( ),∵
),∵ 为等腰直角三角形,∴|PF2|=|F1F2|,
为等腰直角三角形,∴|PF2|=|F1F2|, ,故选D.
,故选D.
考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程 表示焦点在
表示焦点在 轴的双曲线,则
轴的双曲线,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 ,
,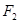 是椭圆
是椭圆 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若 为椭圆
为椭圆 上一点,且
上一点,且 的周长为14,则椭圆
的周长为14,则椭圆 的离心率
的离心率 为
为
A.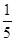 | B. | C. | D. |
设抛物线顶点在坐标原点,,准线方程为 ,则抛物线方程是( )
,则抛物线方程是( )
A. | B. | C. | D. |
已知点 、
、 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、 两点,若
两点,若 为锐角三角形,则该双曲线的离心率
为锐角三角形,则该双曲线的离心率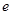 的取值范围是
的取值范围是
A. | B. | C.(1,2) | D. |
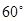 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B.  C.
C.  D.
D. 
 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( ) (p >0)的焦点F恰好是双曲线C2:
(p >0)的焦点F恰好是双曲线C2: (a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
(a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为



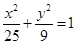 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设 ,则
,则 等于( )
等于( ) B.
B.  C.
C.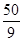 D.
D. 