题目内容
已知 是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引
是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引 的平分线的垂线,垂足为P,则点P的轨迹是
的平分线的垂线,垂足为P,则点P的轨迹是
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
B
解析试题分析:利用已知条件判断出△AQF1为等腰三角形,利用双曲线的定义及等量代换得到AF2=2a,利用三角形的中位线得到OP=a,利用圆的定义判断出点的轨迹.解:设O为F1F2的中点,延长F1P交QF2于A,连接OP,据题意知△AQF1为等腰三角形,所以QF1=QA,∵|QF1-QF2|=2a,∴∵|QA-QF2|=2a,即AF2=2a,∵OP为△F1F2A的中位线,∴OP=a,故点P的轨迹为以O为圆心,以a为半径的圆,故选B
考点:双曲线
点评:本题考查双曲线的定义、原点定义及等量代换的数学方法、三角形的中位线性质

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
过双曲线的一个焦点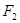 作垂直于实轴的弦
作垂直于实轴的弦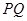 ,
,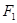 是另一焦点,若∠
是另一焦点,若∠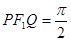 ,则双曲线的离心率
,则双曲线的离心率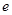 等于( )
等于( )
A. | B.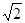 | C.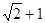 | D.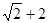 |
在抛物线 上,横坐标为
上,横坐标为 的点到焦点的距离为
的点到焦点的距离为 ,则
,则 的值为( )
的值为( )
| A.0.5 | B.1 | C.2 | D.4 |
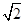 ,则m6+ m4的值为( )
,则m6+ m4的值为( )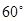 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B.  C.
C.  D.
D. 
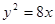 相切倾斜角为
相切倾斜角为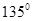 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D.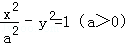 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则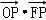 的取值范围为
的取值范围为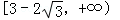
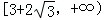
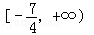
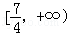
 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( ) (p >0)的焦点F恰好是双曲线C2:
(p >0)的焦点F恰好是双曲线C2: (a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
(a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为


