题目内容

17．已知函数f（x）=$\left\{\begin{array}{l}{\frac{x+1}{x-1}，x≤0}\\{f（x-1），x＞0}\end{array}\right.$，则函数g（x）=f（x）-ex+a的零点个数不可能是（　　）
A．0B．1C．2D．3

分析 函数g（x）=f（x）-ex+a的零点个数可化为函数f（x）与函数y=ex+a的交点的个数；作函数f（x）=$\left\{\begin{array}{l}{\frac{x+1}{x-1}，x≤0}\\{f（x-1），x＞0}\end{array}\right.$与函数y=ex-a的图象，数形结合求解．

解答 解：函数g（x）=f（x）-ex+a的零点个数可化为
函数f（x）与函数y=ex+a的交点的个数；
作函数f（x）=$\left\{\begin{array}{l}{\frac{x+1}{x-1}，x≤0}\\{f（x-1），x＞0}\end{array}\right.$与函数y=ex-a的图象如下，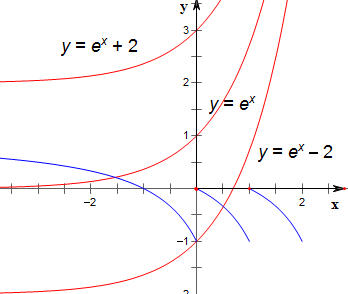

结合图象可知，
当a=2，0，-2时，函数g（x）=f（x）-ex+a的零点个数分别是2，1，0；
故选D．

点评 本题考查了学生的作图能力及图象的变换，同时考查了函数的零点的个数的判断，属于中档题．

练习册系列答案
相关题目
7．设数列{an}的前n项和为Sn，满足Sn=an+1-n•2n+3-4，n∈N*，且a1，S2，2a3+4成等比数列．
（Ⅰ）求a1，a2，a3的值；          
（Ⅱ）设bn=$\frac{a_n}{2^n}$，n∈N*，求{an}的通项公式．
8．证明f（x）=x+$\frac{2}{x}$在（$\sqrt{2}$，+∞）上为增函数．
5．6个儿童分坐两行，每行3人面对着做游戏，其中甲、乙二人既不对面，又不相邻的坐法有384种．（用数字作答）
12．已知函数f（x）对任意x∈R满足f（x+1）=f（x-1），且f（x）是偶函数，当x∈[-1，0]时，f（x）=-x2+1，若方程f（x）=a|x|至少有4个相异实根，则实数a的取值范围是[0，4-2$\sqrt{3}$]．
2．设集合U={1，2，3，4，5}，A={1，3}，B={2，3，4}，则（CUA）∩（CUB）=（　　）
A．{1}B．{5}C．{2，4}D．{1，2，4，5}
9．甲和乙等五名志愿者被随机地分到A、B、C三个不同的岗位服务，每个岗位至少有一名志愿者．若甲和乙不在同一岗位服务，则不同的分法有138种．（用数字作答）
6．设函数y=f（x）定义在实数集R上，则函数y=f（1-x）与y=f（x-1）的图象关于（　　）
A．直线y=0对称B．直线x=0对称C．直线y=1对称D．直线x=1对称
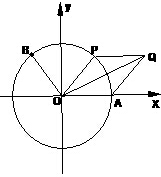7．如图，点A是单位圆与x轴正半轴的交点，B（-$\frac{3}{5}$，$\frac{4}{5}$）．
（I）若∠AOB=α，求cosα+sinα的值；
（II）设点P为单位圆上的一个动点，点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$．若∠AOP=2θ，$\frac{π}{6}≤θ≤\frac{π}{2}$表示|$\overrightarrow{OQ}$|，并求|$\overrightarrow{OQ}$|的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网