题目内容
12.已知函数f(x)对任意x∈R满足f(x+1)=f(x-1),且f(x)是偶函数,当x∈[-1,0]时,f(x)=-x2+1,若方程f(x)=a|x|至少有4个相异实根,则实数a的取值范围是[0,4-2$\sqrt{3}$].分析 由题意可判断函数数f(x)的周期T=2,从而作f(x)与g(x)=a|x|的图象,结合图象可知a≥0;且当在(1,3)上相切时取得另一个临界值,利用导数求出此时的a,即可得到实数a的取值范围.
解答 解:由题意知,函数f(x)的周期T=2,
且f(x)是偶函数,当x∈[-1,0]时,f(x)=-x2+1;
作f(x)与g(x)=a|x|的图象如下,
结合图象可知,a≥0;
当在(1,3)上相切时,
f(x)=-(x-2)2+1,f′(x)=-2(x-2),
故-2(x-2)=$\frac{-(x-2)^{2}+1}{x}$,
解得,x=$\sqrt{3}$;
故a=f′($\sqrt{3}$)=-2($\sqrt{3}$-2)=4-2$\sqrt{3}$;
故实数a的取值范围是[0,4-2$\sqrt{3}$].
故答案为:[0,4-2$\sqrt{3}$].
点评 本题考查了方程的根与函数的图象的关系应用及导数的几何意义的应用,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
2.等比数列{an}的首项为1,公比为q,前n项和记为S,由原数列各项的倒数组成一个新数列{$\frac{1}{{a}_{n}}$},则{$\frac{1}{{a}_{n}}$}的前n项之和S′是( )
| A. | $\frac{1}{S}$ | B. | $\frac{1}{{q}^{n}S}$ | C. | $\frac{{q}^{n}}{S}$ | D. | $\frac{S}{{q}^{n-1}}$ |
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=$\frac{x}{2}$+y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
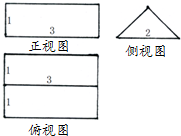

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
7.P是双曲线$\frac{x^2}{4}$-y2=1右支(在第一象限内)上的任意一点,A1,A2分别是左右顶点,O是坐标原点,直线PA1,PO,PA2的斜率分别为k1,k2,k3,则斜率之积k1k2k3的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{8}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{2}$) |
4.对于函数f(x)=eax-lnx,(a是实常数),下列结论正确的一个是( )
| A. | a=1时,B有极大值,且极大值点(1,3) | |
| B. | a=2时,A有极小值,且极小值点x0∈(0,$\frac{1}{4}$) | |
| C. | a=$\frac{1}{2}$时,D有极小值,且极小值点x0∈(1,2) | |
| D. | a<0时,C有极大值,且极大值点x0∈(-∞,0) |
1.已知i是虚数单位,则复数z=i2015的虚部是( )
| A. | 0 | B. | -1 | C. | 1 | D. | -i |