题目内容
5.6个儿童分坐两行,每行3人面对着做游戏,其中甲、乙二人既不对面,又不相邻的坐法有384种.(用数字作答)分析 由于甲、乙是特殊元素,可先安排甲、乙,分两种情况:甲坐两端,或甲在中间两个位上找一个位子坐下,根据分类计数原理可得答案.
解答 解:由于甲、乙是特殊元素,可先安排甲、乙,分两种情况:
(1)甲坐两端,可从四个位中选一个坐下,有$A_4^1$种,由于乙不与甲坐对面和相邻,在其他3个位中选一个坐下有$A_3^1$种,其余4人有$A_4^4$种,此类有$A_4^1A_3^1A_4^4$种方法.
(2)甲在中间两个位上找一个位子坐下,有$A_2^1$种,乙应在其他两个位上找一个位子坐下有$A_2^1$种,其余4人有$A_4^4$种坐法.此类坐法有$A_2^1A_2^1A_4^4$种.
所以满足条件的坐法共有$A_4^1A_3^1A_4^4+A_2^1A_2^1A_4^4$=384(种).
故答案为:384.
点评 本题考查了分类和分步计数原理,特殊元素优先安排原则,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
20.以下是某个几何体的三视图(单位:cm),则该几何体的体积是( )
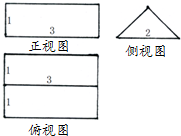

| A. | 2cm3 | B. | 3cm3 | C. | 4cm3 | D. | 5cm3 |
10.已知集合A={x||x+1≤2},B={x|y=lg(x2-x-2)},则A∩∁RB( )
| A. | [-1,1] | B. | [-3,-1] | C. | (-1,1] | D. | [-3,-1) |
 如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知 AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.