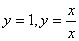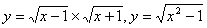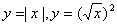题目内容
已知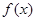 是定义在
是定义在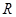 上的奇函数. 当
上的奇函数. 当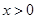 时,
时,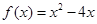 ,则不等式
,则不等式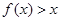 的解集用区间表示为
的解集用区间表示为
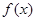 是定义在
是定义在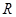 上的奇函数. 当
上的奇函数. 当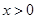 时,
时,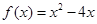 ,则不等式
,则不等式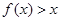 的解集用区间表示为
的解集用区间表示为 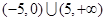
∵当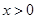 时,
时,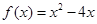 ,令
,令 ,
, ,∴
,∴ ,又
,又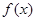 是定义在
是定义在 上的奇函数,∴
上的奇函数,∴ ,∴
,∴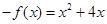 ,即
,即 时,
时,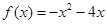 . 要
. 要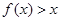 ,则
,则
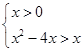 或
或 或
或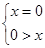 ,解得
,解得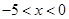 或
或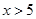 ,∴不等式
,∴不等式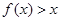 的解集用区间为
的解集用区间为
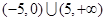 .
.
【考点定位】分段函数,函数的奇偶性,一元二次不等式的解法. 考查计算能力.中等题.
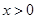 时,
时,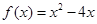 ,令
,令 ,
, ,∴
,∴ ,又
,又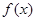 是定义在
是定义在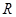 上的奇函数,∴
上的奇函数,∴ ,∴
,∴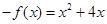 ,即
,即 时,
时,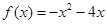 . 要
. 要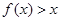 ,则
,则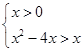 或
或 或
或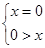 ,解得
,解得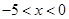 或
或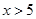 ,∴不等式
,∴不等式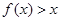 的解集用区间为
的解集用区间为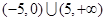 .
.【考点定位】分段函数,函数的奇偶性,一元二次不等式的解法. 考查计算能力.中等题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
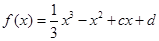
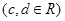 ,其图象为曲线
,其图象为曲线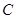 ,点
,点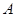 为曲线
为曲线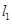 与曲线
与曲线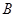 ,在点
,在点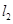 .
.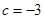 时,求函数
时,求函数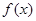 的单调区间;
的单调区间;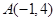 时,
时,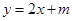 ,求实数
,求实数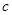 和
和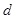 的值;
的值;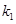 、
、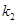 ,试问:是否存在常数
,试问:是否存在常数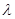 ,使得
,使得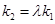 ?若存在,求出
?若存在,求出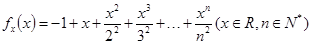 ,证明:
,证明: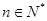 ,存在唯一的
,存在唯一的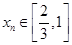 ,满足
,满足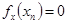 ;
;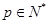 ,由(Ⅰ)中
,由(Ⅰ)中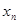 构成的数列
构成的数列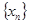 满足
满足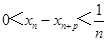 .
.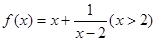 在
在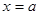 处取最小值, 则
处取最小值, 则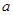 =( )
=( )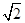
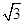
 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 (千克/年);当
(千克/年);当 时,
时, (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, (千克/年).
(千克/年). 时,求函数
时,求函数 的表达式;
的表达式; 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.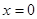 是函数
是函数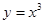 的极值点;
的极值点;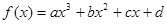 有极值点的充要条件是
有极值点的充要条件是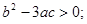
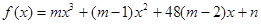 在区间
在区间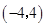 上单调递减.
上单调递减.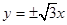 ,则其离心率为2.
,则其离心率为2.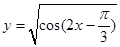 的定义域是 .
的定义域是 .