题目内容
如图,已知多面体 的底面
的底面 是边长为
是边长为 的正方形,
的正方形, 底面
底面 ,
, ,且
,且 .
.
(Ⅰ)求多面体 的体积;
的体积;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.

 的底面
的底面 是边长为
是边长为 的正方形,
的正方形, 底面
底面 ,
, ,且
,且 .
.(Ⅰ)求多面体
 的体积;
的体积;(Ⅱ)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面
 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅰ)(Ⅰ)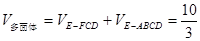 .
.
(Ⅱ)设直线 与平面
与平面 所成角为
所成角为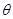 ,
,
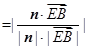
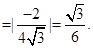
(Ⅲ)利用三角形中位线定理,取线段DC的中点 ,连接即为所求.
,连接即为所求.

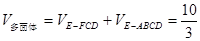 .
. (Ⅱ)设直线
 与平面
与平面 所成角为
所成角为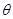 ,
,
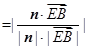
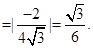
(Ⅲ)利用三角形中位线定理,取线段DC的中点
 ,连接即为所求.
,连接即为所求. 
试题分析:(Ⅰ)(Ⅰ)连接ED,利用“分割法”计算得
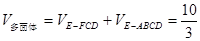 .
.(Ⅱ)以点A为原点,AB所在的直线为
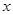 轴,AD所在的直线为
轴,AD所在的直线为 轴,建立空间直角坐标系.确定得到A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),及
轴,建立空间直角坐标系.确定得到A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),及 .
.利用
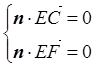 确定平面
确定平面 的一个法向量为
的一个法向量为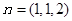 .
.设直线
 与平面
与平面 所成角为
所成角为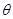 ,
,
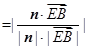
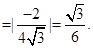
(Ⅲ)取线段DC的中点
 ;连接
;连接 ,则直线
,则直线 即为所求.
即为所求. 试题解析:(Ⅰ)如图,连接ED,
∵
 底面
底面 且
且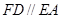 ,∴
,∴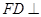 底面
底面 ,
,∴
 ,
,∵
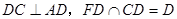 ,
,∴
 面
面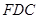 , 1分
, 1分∴
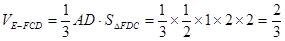 , 2分
, 2分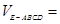

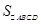
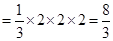 , 3分
, 3分∴多面体
 的体积
的体积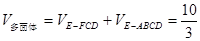 . 5分
. 5分(Ⅱ)以点A为原点,AB所在的直线为
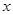 轴,AD所在的直线为
轴,AD所在的直线为 轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),
轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),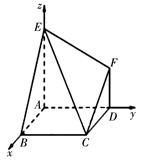
所以
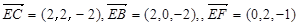 7分
7分设平面ECF的法向量为
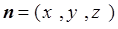 ,
,则
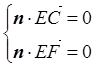 得:
得: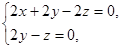
取y=1,得平面
 的一个法向量为
的一个法向量为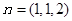 9分
9分设直线
 与平面
与平面 所成角为
所成角为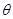 ,
,所以

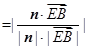
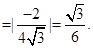 11分
11分 (Ⅲ)取线段CD的中点
 ;连接
;连接 ,直线
,直线 即为所求. 12分
即为所求. 12分图上有正确的作图痕迹 13分


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
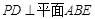 ;
; 的平面角的正弦值.
的平面角的正弦值. 的正方形
的正方形 中,
中, 分别为
分别为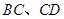 的中点,
的中点, 分别为
分别为 的中点,现沿
的中点,现沿 折叠,使
折叠,使 三点重合,重合后的点记为
三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.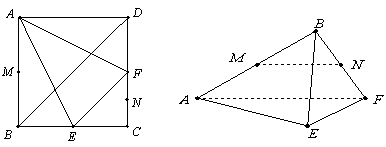
 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 平面
平面 ;
; 的体积.
的体积.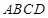 -
- ,
, =2,
=2,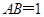 ,
,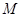 ,
,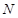 分别在
分别在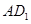 ,
,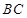 上移动,且始终保持
上移动,且始终保持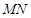 ∥平面
∥平面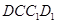 ,设
,设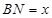 ,
,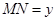 ,则函数
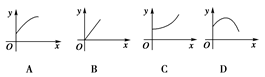
,则函数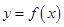 的图象大致是( )
的图象大致是( )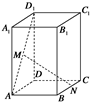
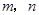 ,两个平面
,两个平面 .下面四个命题中不正确的是( )
.下面四个命题中不正确的是( )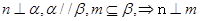
 ,
, ,
, ;
;
 ,
,

 、
、 和平面
和平面 ,若
,若 ,则“
,则“ ”是“
”是“ ”的( )
”的( ) 及其三视图中的主视图和左视图如图9所示,则棱
及其三视图中的主视图和左视图如图9所示,则棱 的长为_________.
的长为_________.
 a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l
a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l 是空间三条不同的直线,
是空间三条不同的直线, 是空间中不同的平面,则下列命题中不正确的是( )
是空间中不同的平面,则下列命题中不正确的是( ) ,
, ,则
,则
 ,
, ,则
,则
 且
且 是
是 在
在 内的射影,若
内的射影,若 ,则
,则
 时,若
时,若 ,则
,则