题目内容
已知直线 与椭圆
与椭圆
 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量 与向量
与向量 互相垂直(其中
互相垂直(其中 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值.
 与椭圆
与椭圆
 相交于A、B两点.
相交于A、B两点. (1)若椭圆的离心率为
 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;(2)若向量
 与向量
与向量 互相垂直(其中
互相垂直(其中 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值.(1)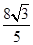 (2)
(2)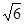
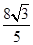 (2)
(2)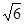
(1)(6分)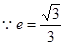 ,2c=2,即
,2c=2,即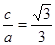 ∴
∴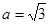 则
则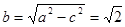
∴椭圆的方程为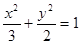 ,
,
将y ="-" x+1代入消去y得: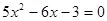
设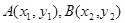
∴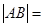
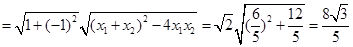
(2)(7分)设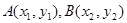
 ,即
,即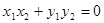
由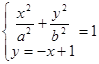 ,
,
消去y得: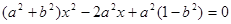
由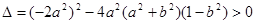 ,
,
整理得: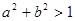
又 ,
,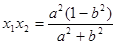
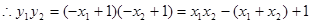
由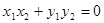 ,得:
,得: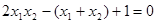
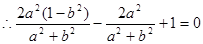 ,
,
整理得: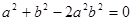
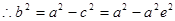
代入上式得: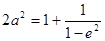 ,
,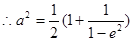
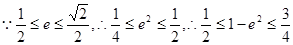
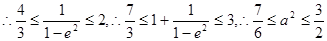
条件适合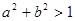 ,
,
由此得: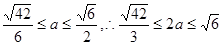
故长轴长的最大值为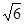 .
.
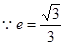 ,2c=2,即
,2c=2,即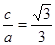 ∴
∴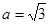 则
则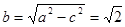
∴椭圆的方程为
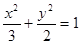 ,
,将y ="-" x+1代入消去y得:
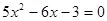
设
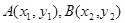
∴
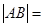
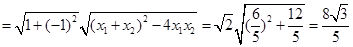
(2)(7分)设
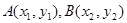
 ,即
,即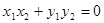
由
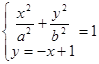 ,
,消去y得:
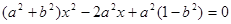
由
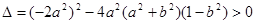 ,
,整理得:
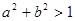
又
 ,
,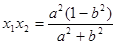
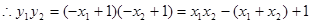
由
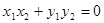 ,得:
,得: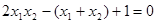
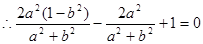 ,
,整理得:
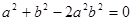
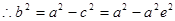
代入上式得:
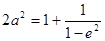 ,
,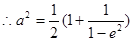
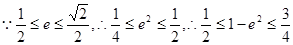
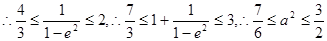
条件适合
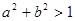 ,
,由此得:
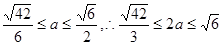
故长轴长的最大值为
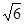 .
.
练习册系列答案
相关题目
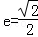 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.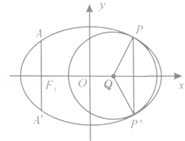
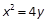 相切于点P(2,1),且与
相切于点P(2,1),且与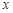 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .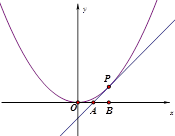
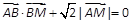 ,求点M的轨迹C;
,求点M的轨迹C;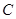 的两个焦点为
的两个焦点为 ,
, ,一个顶点式
,一个顶点式 ,则
,则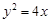 的焦点为
的焦点为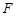 ,点
,点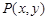 为该抛物线上的动点,又点
为该抛物线上的动点,又点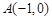 ,
,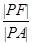 的取值范围是 .
的取值范围是 .  右焦点为
右焦点为 ,方程
,方程 的两实根分别为
的两实根分别为 ,则
,则 ( )
( ) 内
内 外
外 的中心在坐标原点,对称轴为坐标轴,焦点在
的中心在坐标原点,对称轴为坐标轴,焦点在 轴上,有一个顶点为
轴上,有一个顶点为 ,
, .
. 作直线
作直线 与椭圆
与椭圆 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围.
的取值范围.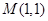 作斜率为
作斜率为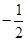 的直线与椭圆
的直线与椭圆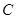 :
: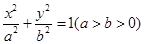 相交于
相交于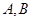 ,若
,若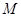 是线段
是线段 的中点,则椭圆
的中点,则椭圆