题目内容
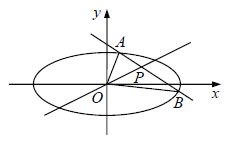
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
【答案】( Ⅰ)存在;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)设出直线![]() 方程为
方程为![]() ,代入椭圆方程得关于
,代入椭圆方程得关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,则可得
,则可得![]() ,利用
,利用![]() 可建立
可建立![]() 的关系,即
的关系,即![]() ,上面的一元二次方程有两个不等实根,即判别式
,上面的一元二次方程有两个不等实根,即判别式![]() ,由此可得
,由此可得![]() 的范围.注意特殊情形的讨论,最后由直线
的范围.注意特殊情形的讨论,最后由直线![]() 和直线
和直线![]() 的倾斜角互补,即斜率和为0可求得
的倾斜角互补,即斜率和为0可求得![]() ,若不能求出
,若不能求出![]() ,说明不存在);(Ⅱ)利用(Ⅰ)得直线
,说明不存在);(Ⅱ)利用(Ⅰ)得直线![]() 方程为
方程为![]() ,关键是由表示出
,关键是由表示出![]() ,
, ![]() ,这是
,这是![]() 的函数,可函数知识易求最值.
的函数,可函数知识易求最值.
试题解析:
(Ⅰ)存在.
由题意直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程
的方程
是![]()
代入![]() 得:
得:
![]()
![]()
![]() .(1)
.(1)
设![]() ,
,![]() ,则
,则![]() ,即
,即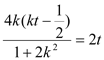 ,
,
解得:![]() ,
,
此时方程(1)即![]()
![]()
![]()
由![]() 解得,
解得,![]() ,
,
(或由![]() 解得,
解得,![]() )
)
当![]() 时,显然不符合题意;
时,显然不符合题意;
当![]() 时,设直线
时,设直线![]() 的斜率为
的斜率为![]() ,只需
,只需![]() ,
,
即![]() ,解得
,解得![]() ,均符合题意.
,均符合题意.
(Ⅱ)由(1)知![]() 的方程是
的方程是![]() ,
,
所以![]() ,
,
![]()
![]()
![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() .
.
点晴:解析几何中存在性问题的求解方法:
1.通常采用“肯定顺推法”,将不确定性问题明朗化,其步骤为:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于特定参数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则(点、直线、曲线或参数)不存在.
2.反证法与验证法也是求解存在性问题的常用方法.

练习册系列答案
相关题目