题目内容
【题目】.(本小题满分12分)
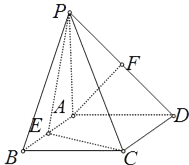
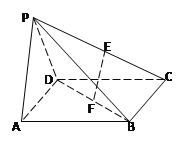
如图,四棱锥P—ABCD中,底面ABCD是边长为![]() 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=![]() AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
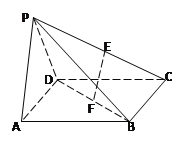
【答案】解:(Ⅰ)证明:连接AC,则F是AC的中点,
E为PC的中点,故在![]() CPA中,EF//PA,
CPA中,EF//PA,
且PA![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,∴EF//平面PAD
平面PAD,∴EF//平面PAD
(Ⅱ)取AD的中点M,连接PM,∵PA=PD,∴PM⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴PM⊥平面ABCD.
在直角![]() PAM中,求得PM=
PAM中,求得PM=![]() ,∴
,∴![]()
![]() PM=
PM=![]()
【解析】试题分析:解:(Ⅰ)证明:连接AC,则F是AC的中点,
E为PC的中点,故在![]() CPA中,EF//PA,
CPA中,EF//PA,
且PA![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD,∴EF//平面PAD
平面PAD,∴EF//平面PAD
(Ⅱ)取AD的中点M,连接PM,∵PA=PD,∴PM⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴PM⊥平面ABCD.
在直角![]() PAM中,求得PM=
PAM中,求得PM= ![]() ,∴
,∴![]()
![]() PM=
PM=![]()

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目