题目内容
(本小题满分12分)
如图,在多面体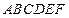 中,四边形
中,四边形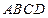 是正方形,
是正方形,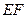 ∥
∥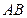 ,
,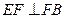 ,
,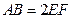 ,
,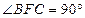 ,
,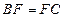 ,
,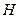 为
为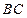 的中点。
的中点。
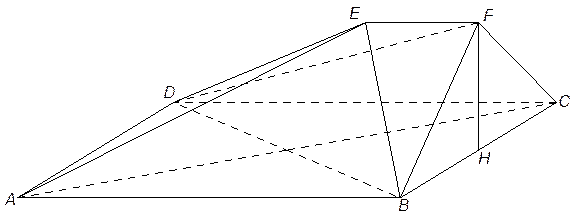
(Ⅰ)求证: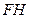 ∥平面
∥平面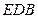 ;
;
(Ⅱ)求证: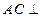 平面
平面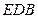 ;
;
(Ⅲ)求二面角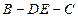 的大小。
的大小。
如图,在多面体
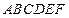 中,四边形
中,四边形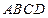 是正方形,
是正方形,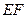 ∥
∥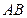 ,
,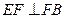 ,
,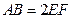 ,
,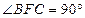 ,
,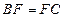 ,
,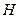 为
为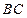 的中点。
的中点。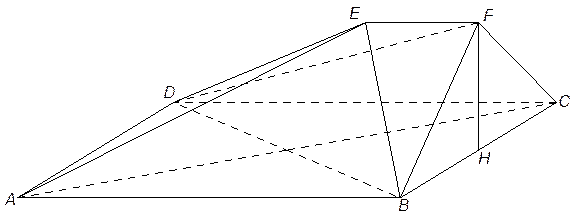
(Ⅰ)求证:
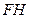 ∥平面
∥平面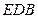 ;
;(Ⅱ)求证:
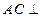 平面
平面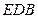 ;
;(Ⅲ)求二面角
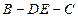 的大小。
的大小。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
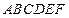 中,四边形
中,四边形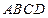 是正方形,
是正方形,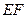 ∥
∥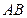 ,
,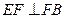 ,
,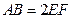 ,
,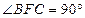 ,
,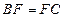 ,
,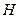 为
为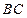 的中点。
的中点。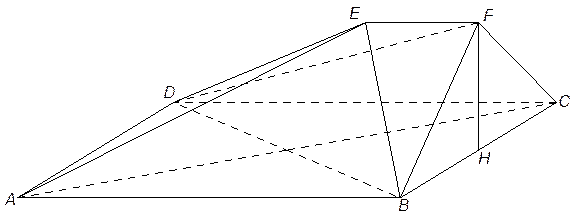
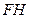 ∥平面
∥平面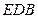 ;
;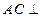 平面
平面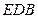 ;
;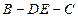 的大小。
的大小。
 阅读快车系列答案
阅读快车系列答案