题目内容
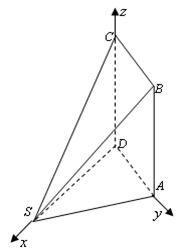
(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,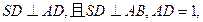
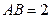 ,
,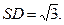
(1)求证:CD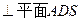 ;
;
(2)求AD与SB所成角的余弦值;
(3)求二面角A—SB—D的余弦值.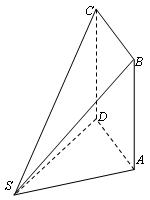
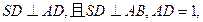
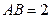 ,
,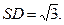
(1)求证:CD
 ;
;(2)求AD与SB所成角的余弦值;
(3)求二面角A—SB—D的余弦值.

(1)证明见解析。
(2)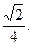
(3)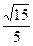
(2)
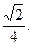
(3)
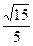
(1)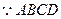 是矩形,
是矩形,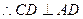 --------------1分
--------------1分
又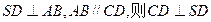 -------------2分
-------------2分
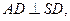 -------------3分
-------------3分
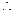 CD
CD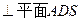 -------------4分
-------------4分
(2)由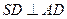 ,及(I)结论可知DA、DC、DS
,及(I)结论可知DA、DC、DS
两两互相垂直,
建立如图所示的空间直角坐标系
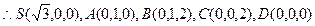 --------------5分
--------------5分
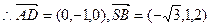 --------------6分
--------------6分
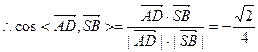 --------------7分
--------------7分
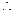 AD与SB所成的角的余弦为
AD与SB所成的角的余弦为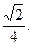 --------------8分
--------------8分
(3)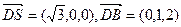 设面SBD的一个法向量为
设面SBD的一个法向量为
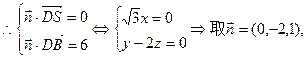 --------------9分
--------------9分
又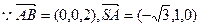
∴设面DAB的一个法向量为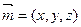
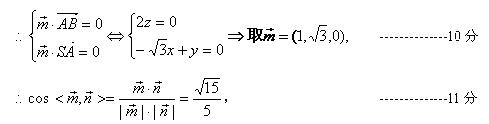
所以所求的二面角的余弦为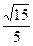 …………11分
…………11分
解法二
(1)同解法一
(2)矩形ABCD,∴AD//BC,即BC=a,
∴要求AD与SB所成的角,即求BC与SB所成的角 …………5分
在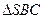 中,由(1)知,SD⊥面ABCD。
中,由(1)知,SD⊥面ABCD。
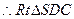 中,
中,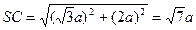
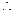 CD是CS在面ABCD内的射
CD是CS在面ABCD内的射 影,且
影,且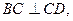
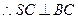
 --------------6分
--------------6分
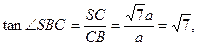
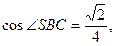 ----------8分
----------8分
从而SB与AD的成的角的余弦为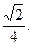
(3)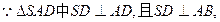
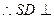 面ABCD.
面ABCD.
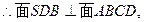 BD为面SDB与面ABCD的交线.
BD为面SDB与面ABCD的交线.
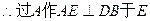
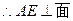 SDB
SDB
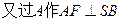 于F,连接EF,
于F,连接EF,
从而得: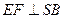
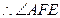 为二面角A—SB—D的平面角 ------10分
为二面角A—SB—D的平面角 ------10分
在矩形ABCD中,对角线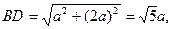
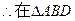 中,
中,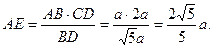
由(2)知在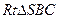 ,
,
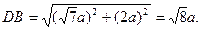
而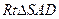 中,SA=a,且AB=2a,
中,SA=a,且AB=2a,
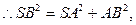
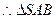 为等腰直角三角形且
为等腰直角三角形且 为直角,
为直角,
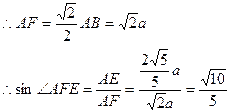
所以所求的二面角的余弦为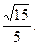 --------------12分
--------------12分
 是矩形,
是矩形,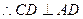 --------------1分
--------------1分又
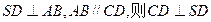 -------------2分
-------------2分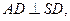 -------------3分
-------------3分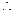 CD
CD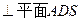 -------------4分
-------------4分(2)由
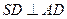 ,及(I)结论可知DA、DC、DS
,及(I)结论可知DA、DC、DS两两互相垂直,
建立如图所示的空间直角坐标系

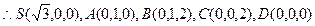 --------------5分
--------------5分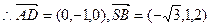 --------------6分
--------------6分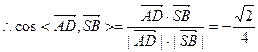 --------------7分
--------------7分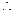 AD与SB所成的角的余弦为
AD与SB所成的角的余弦为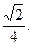 --------------8分
--------------8分(3)
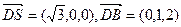 设面SBD的一个法向量为
设面SBD的一个法向量为
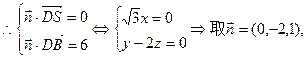 --------------9分
--------------9分又
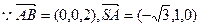
∴设面DAB的一个法向量为
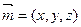
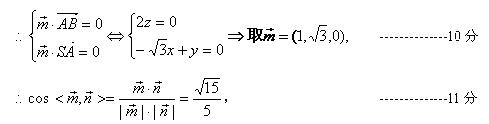
所以所求的二面角的余弦为
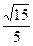 …………11分
…………11分解法二
(1)同解法一
(2)矩形ABCD,∴AD//BC,即BC=a,
∴要求AD与SB所成的角,即求BC与SB所成的角 …………5分
在
 中,由(1)知,SD⊥面ABCD。
中,由(1)知,SD⊥面ABCD。 中,
中,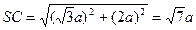
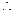 CD是CS在面ABCD内的射
CD是CS在面ABCD内的射 影,且
影,且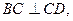
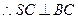
 --------------6分
--------------6分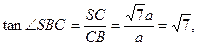
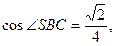 ----------8分
----------8分从而SB与AD的成的角的余弦为
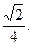
(3)
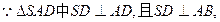
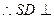 面ABCD.
面ABCD. 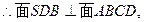 BD为面SDB与面ABCD的交线.
BD为面SDB与面ABCD的交线.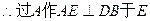
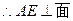 SDB
SDB 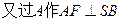 于F,连接EF,
于F,连接EF, 从而得:
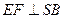
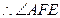 为二面角A—SB—D的平面角 ------10分
为二面角A—SB—D的平面角 ------10分在矩形ABCD中,对角线
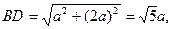
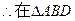 中,
中,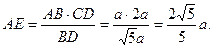
由(2)知在
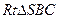 ,
,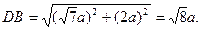
而
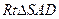 中,SA=a,且AB=2a,
中,SA=a,且AB=2a,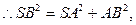
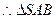 为等腰直角三角形且
为等腰直角三角形且 为直角,
为直角,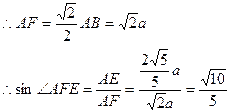
所以所求的二面角的余弦为
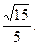 --------------12分
--------------12分
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
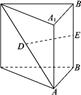
 中,AB=1,AC=2,
中,AB=1,AC=2,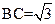 ,D,E分别是
,D,E分别是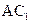 和
和 的中点.
的中点.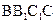 所成的角.
所成的角.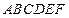 中,四边形
中,四边形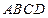 是正方形,
是正方形,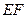 ∥
∥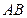 ,
,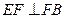 ,
,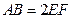 ,
,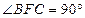 ,
,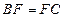 ,
,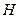 为
为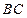 的中点。
的中点。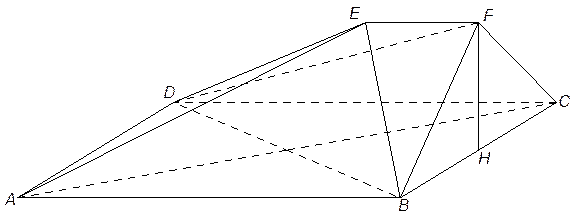
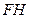 ∥平面
∥平面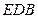 ;
;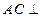 平面
平面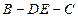 的大小。
的大小。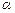 、
、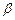 ,直线a、b,若
,直线a、b,若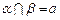 ,
,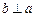 ,则
,则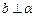 ;
; 两全等的四棱柱为直四棱柱;
两全等的四棱柱为直四棱柱;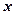 ,其余各条棱得长都为
,其余各条棱得长都为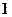 ,则这个四面体的体积最大时,
,则这个四面体的体积最大时,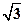
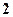
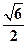
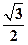
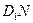 所成的角,则
所成的角,则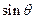 =" " ( )
=" " ( ) 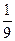
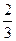
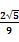
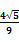
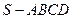 中,
中,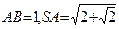 ,则
,则 两点间的球面距离为 .
两点间的球面距离为 . 是边长为
是边长为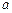 的正
的正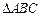 内的一点,
内的一点,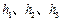 ,则
,则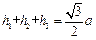 ;类比到空间,设
;类比到空间,设 内的一点,则
内的一点,则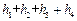 = .
= .