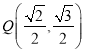题目内容
【题目】已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
(1)求椭圆C的标准方程;
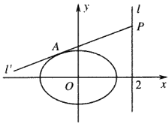
(2)设A,B是x轴上不同的两点,点A(异于坐标原点)在椭圆C内,点B在椭圆C外.若过点B作斜率不为0的直线与C相交于P,Q两点,且满足∠PAB+∠QAB=180°.证明:点A,B的横坐标之积为定值.
【答案】(1)![]() y2=1;(2)见解析
y2=1;(2)见解析
【解析】
(1)由题意离心率的值及三角形OMN的面积和a,b,c之间的关系求出a,b的值,进而求出椭圆的方程;
(2)作点P关于x轴的对称点![]() ,由椭圆的对称性可知∠PAB=∠
,由椭圆的对称性可知∠PAB=∠![]() AB,∠QBA=∠
AB,∠QBA=∠![]() BA,所以
BA,所以![]() ,A,Q三点共线,设
,A,Q三点共线,设![]() Q,A,B的坐标,设直线
Q,A,B的坐标,设直线![]() Q的方程与椭圆联立求出两根之和及两根之积,因为∠QBA=∠
Q的方程与椭圆联立求出两根之和及两根之积,因为∠QBA=∠![]() BA,所以
BA,所以![]() ,求出两条直线的斜率,求出A,B的乘积为定值.
,求出两条直线的斜率,求出A,B的乘积为定值.
解:(1)由题意可得: ,解得:a2=4,b2=1,
,解得:a2=4,b2=1,
所以椭圆C的标准方程:![]() y2=1;
y2=1;
(2)证明:作点P关于x轴的对称点![]() ,由椭圆的对称性可知,
,由椭圆的对称性可知,
点![]() 在椭圆上,且∠PAB=∠
在椭圆上,且∠PAB=∠![]() AB,∠QBA=∠
AB,∠QBA=∠![]() BA,
BA,
因为∠PAB+∠QAB=180°.所以∠![]() AB+∠QAB=180°,
AB+∠QAB=180°,
所以![]() ,A,Q三点共线,
,A,Q三点共线,
由题意可知直线![]() Q不与x轴平行或重合,设直线
Q不与x轴平行或重合,设直线![]() Q的方程为:x=ty+m,(mt≠0),
Q的方程为:x=ty+m,(mt≠0),
设![]() ,
,
联立直线与椭圆的方程:![]() ,消x可得
,消x可得![]() ,
,
则有y1+y2![]() ,y1y2
,y1y2![]() ,
,
因为∠QBA=∠![]() BA,所以
BA,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]()
即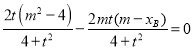 ,
,
解得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故点A,B横坐标之积为定值4.

练习册系列答案
相关题目