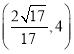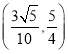题目内容
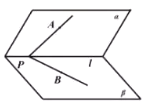
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
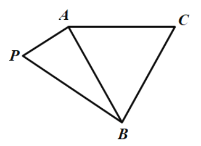
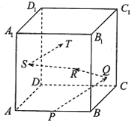
由题意画出图形,分别找出二面角及线面角,结合正切函数的单调性及平面的斜线与平面内所有直线所成角中的最小角是线面角进行大小比较.
解:当PA⊥l,PB⊥l时,δ=φ=θ;
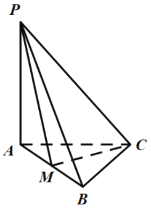
当PA,PB与l均不垂直时,如图:
由已知AB⊥β,可得AB⊥l,过A作AO⊥l,连接OB,则OB⊥l,
可得∠AOB为δ,∠APB=φ,
在平面AOB内,过B作BI⊥AO,则BI⊥α,连接PI,则∠BPI=θ,
在Rt△ABO与Rt△ABP中,可得tanδ![]() ,tanφ
,tanφ![]() ,由AB=AB,PB>OB,
,由AB=AB,PB>OB,
可得tanδ>tanφ,则δ>φ;
PB为平面α的一条斜线,PB与α内所有直线所成角的最小角为θ,即φ>θ.
∴δ>φ>θ.
综上,δ≥φ≥θ.
故选:A.


练习册系列答案
相关题目