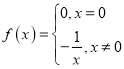题目内容
【题目】已知在平面直角坐标系xOy中,曲线C的参数方程为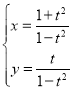 (t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(
(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(![]() )
)![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l交曲线C于A,B两点,交x轴于点P,求![]() 的值.
的值.
【答案】(1)x2﹣4y2=1(![]() ),
),![]() ;(2)8 .
;(2)8 .
【解析】
(1)对曲线C通过消参即可得解,对直线l通过极坐标和直角坐标的互化,即可得解.
(2)求出直线的参数方程为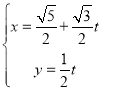 ,将直线方程代入曲线方程,结合韦达定理,再利用直线的标准参数方程中
,将直线方程代入曲线方程,结合韦达定理,再利用直线的标准参数方程中![]() 的几何意义即可得解.
的几何意义即可得解.
(1)曲线C的参数方程为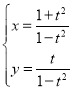 (t为参数),
(t为参数),
转化为直角坐标方程为x2﹣4y2=1(![]() )
)
直线l的极坐标方程为ρcos(![]() )
)![]() .转化为直角坐标方程为:
.转化为直角坐标方程为:![]() .
.
(2)由于直线与x轴的交点坐标为(![]() ),所以直线的参数方程为
),所以直线的参数方程为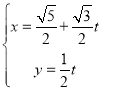 (t为参数),
(t为参数),
代入x2﹣4y2=1得到:![]() ,
,
所以:![]() ,t1
,t1![]() t2=-1,
t2=-1,
则: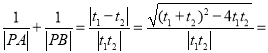 8.
8.

练习册系列答案
相关题目
【题目】有标号分别为1,2,3,4,5,6的6张抗疫宣传海报,要求排成2行3列,则共有_______种不同的排法,如果再要求每列中前面一张的标号比其后面一张的标号小,则共有_______种不同的排法.
【题目】针对某新型病毒,某科研机构已研发出甲乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有![]() 的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占
的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占![]() .
.
产生抗体 | 未产生抗体 | 合计 | |
甲 | |||
乙 | |||
合计 |
(1)根据题中数据,完成列联表;
(2)根据(1)中的列联表,判断能否有![]() 的把握认为甲乙两种疫苗的效果有差异.
的把握认为甲乙两种疫苗的效果有差异.
参考公式: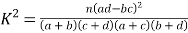 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|