题目内容
【题目】若函数![]() 对
对![]() 、
、![]() ,同时满足:(1)当
,同时满足:(1)当![]() 时有
时有![]() ;(2)当
;(2)当![]() 时有
时有![]() ,则称
,则称![]() 为
为![]() 函数.下列函数中:①
函数.下列函数中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④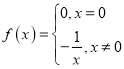 .是
.是![]() 函数的为( )
函数的为( )
A.①②B.②③C.③④D.①④
【答案】A
【解析】
由题意可得![]() 满足是
满足是![]() 上的奇函数,且为增函数,称为
上的奇函数,且为增函数,称为![]() 函数,由函数的奇偶性和单调性与导数之间的关系,分别判断①、②、③、④的函数的奇偶性和单调性,可得所求结论.
函数,由函数的奇偶性和单调性与导数之间的关系,分别判断①、②、③、④的函数的奇偶性和单调性,可得所求结论.
由(1)当![]() 时有
时有![]() ,即为
,即为![]() ,则
,则![]() 为
为![]() 上的奇函数;
上的奇函数;
由(2)当![]() 时有
时有![]() ,即为
,即为![]() ,
,![]() ,
,
可得![]() 为
为![]() 上的增函数,
上的增函数,
则函数![]() 为
为![]() 上的奇函数,且为增函数.
上的奇函数,且为增函数.
由①![]() ,定义域为
,定义域为![]() ,
,![]() ,即
,即![]() 为奇函数,
为奇函数,
又![]() ,可得
,可得![]() 为
为![]() 上的增函数,故①是
上的增函数,故①是![]() 函数;
函数;
②![]() ,定义域为
,定义域为![]() ,
,![]() ,即
,即![]() 为奇函数,
为奇函数,
又![]() ,可得
,可得![]() 为
为![]() 上的增函数,故②是
上的增函数,故②是![]() 函数;
函数;
③![]() ,定义域为
,定义域为![]() ,
,![]() ,可得
,可得![]() 为偶函数,故③不是
为偶函数,故③不是![]() 函数;
函数;
④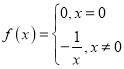 ,定义域为
,定义域为![]() ,
,![]() 时,
时,![]() ,可得
,可得![]() 为奇函数,
为奇函数,
又![]() 在
在![]() ,
,![]() 上单调递增,但在
上单调递增,但在![]() 上不为增函数,比如
上不为增函数,比如![]() ,故④不是
,故④不是![]() 函数.
函数.
故选:A.

练习册系列答案
相关题目
【题目】2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善生存环境质量.某部门在某小区年龄处于区间![]() 内的人中随机抽取
内的人中随机抽取![]() 人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
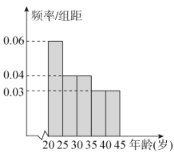
(1)求![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(3)从年龄段在![]() 的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间
的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间![]() 中的概率.
中的概率.
组数 | 分组 | “环保族”人数 | 占本组频率 |
第一组 |
| 45 | 0.75 |
第二组 |
| 25 |
|
第三组 |
|
| 0.5 |
第四组 |
| 3 | 0.2 |
第五组 |
| 3 | 0.1 |