题目内容
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
【答案】差 5 32
【解析】
题设中给出的是第一行数的加法与第二行数的乘法的对应关系,类比到所求的问题中就是第一行数的减法与第二行数的除法之间的对应关系,从而可求规定的值.
题设中给出的计算方法是:
第一行数中两数的和与与第二行数的对应的两数的乘积是匹配的,
因此,若在在第二行找到4096与128,要求它们的商,
可以找出它们在第一行对应的数,即12与7,它们的差(5)在第二行中对应的数(32)即为![]() .
.
故答案为:差,5,32.

【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,在2060岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示:
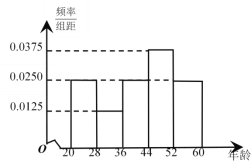
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异?
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会,现从这8人中随机抽2人.记抽到44岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: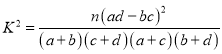 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.