题目内容
【题目】已知椭圆![]() 和圆
和圆![]() ,
,![]() 、
、![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I)根据已知条件求得![]() 和
和![]() 的值,由此可得出椭圆
的值,由此可得出椭圆![]() 的方程;
的方程;
(Ⅱ)将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,由
的方程联立,由![]() 可得出
可得出![]() ,并求出点
,并求出点![]() 的坐标,根据圆的切线的性质可得出直线
的坐标,根据圆的切线的性质可得出直线![]() 的方程为
的方程为![]() ,与直线
,与直线![]() 的方程联立可求得点
的方程联立可求得点![]() 的坐标,求得直线
的坐标,求得直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标,利用三角形的面积公式以及基本不等式可求得
的坐标,利用三角形的面积公式以及基本不等式可求得![]() 面积的最大值.
面积的最大值.
(Ⅰ)由题可知![]() .①
.①
设![]() ,则由
,则由![]() 与圆相切时
与圆相切时![]() ,得
,得![]() ,即
,即![]() .②
.②
将①②代入![]() ,解得
,解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)设点![]() 、
、![]() ,
,
将![]() 代入
代入![]() 得
得![]() .
.
由直线![]() 与椭圆
与椭圆![]() 相切得
相切得![]() ,即
,即![]() ,且
,且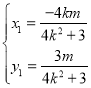 ,
,
由直线![]() 与圆
与圆![]() 相切,设
相切,设![]() ,与
,与![]() 联立得
联立得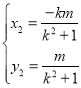 ,
,
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() .
.
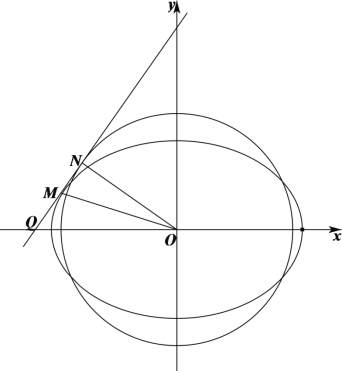
所以![]() 的面积为
的面积为![]()
 ,
,
当且仅当![]() 时等号成立,
时等号成立,
所以![]() 的面积的最大值为
的面积的最大值为![]() .
.

【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.