题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对一切正整数
,且对一切正整数![]() 都有
都有![]() .
.
(1)求证:![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在实数![]() ,使不等式
,使不等式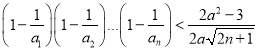 ,对一切正整数
,对一切正整数![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在;
;(3)存在;![]() 的取值范围是
的取值范围是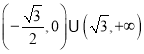 .
.
【解析】
(1)由题得![]() ①,
①,![]() ②,②-①即得
②,②-①即得![]() ;
;
(2)由题得![]() .
.![]() ,再对
,再对![]() 分奇数和偶数两种情况讨论,求出数列
分奇数和偶数两种情况讨论,求出数列![]() 的通项公式;
的通项公式;
(3)令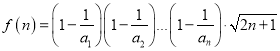
![]() ,判断函数的单调性,求出其最大值,解不等式
,判断函数的单调性,求出其最大值,解不等式![]() 即得解.
即得解.
(1)证明:∵![]() ①,
①,
∴![]() ②
②
由②-①得![]() ,
,
∴![]() .
.
(2)∵![]() ③
③
∴![]() ,④
,④
④-③,得![]() .
.![]()
从而数列![]() 的奇数项依次成等差数列,且首项为
的奇数项依次成等差数列,且首项为![]() ,公差为
,公差为![]() ;
;
数列![]() 的偶数项也依次成等差数列,且首项为
的偶数项也依次成等差数列,且首项为![]() ,公差为
,公差为![]() .
.
在①中令![]() 得
得![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
在③中令![]() 得
得![]() ,∴
,∴![]() .
.
∴当![]() 时,
时,![]() ,
,![]() ;
;
∴当![]()
![]() 时,
时,![]() ,
,![]() ;
;
综上所述,![]() .
.
(3)令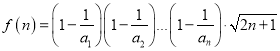
![]() ,则
,则![]()
且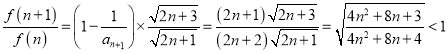
∴![]() ,
,
∴![]() 单调递减,
单调递减,
∴![]() .
.
∴不等式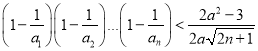 对一切正整数
对一切正整数![]() 都成立等价于
都成立等价于![]() 对一切正整数
对一切正整数![]() 都成立,
都成立,
等价于![]() ,即
,即![]() .
.
∴![]() ,即
,即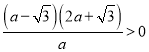 ,
,
解之得![]() ,或
,或![]() .
.
综上所述,存在实数![]() 的适合题意,
的适合题意,![]() 的取值范围是
的取值范围是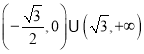 .
.

【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: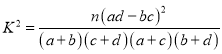 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |