��Ŀ����
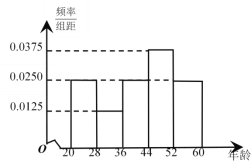
����Ŀ��Ϊ���Ʒ��۹������Ǻ��ȳ���������������Ӧ������٣�������˳�̨��ϵ�з��۵�������.ij���ⶨ��̨�����������������ߡ�.Ϊ�˽����Ƕԡ��������������ߡ���̬�ȣ���2060�����Ⱥ���������100�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�֡����������������������ͳ�ƽ����ͼ��ʾ��
���� |
|
|
|
|
|
֧�ֵ����� | 15 | 5 | 15 | 28 | 17 |
��1��������ͳ��������![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��44��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��������������ߡ���֧�ֶ��в��죿
�����������ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��44��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��������������ߡ���֧�ֶ��в��죿
44������ | 44�꼰44������ | �ܼ� | |
֧�� | |||
��֧�� | |||
�ܼ� |
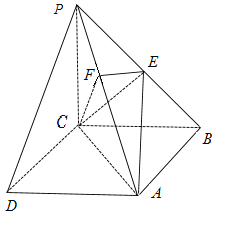
��2������44��Ϊ�ֽ�㣬�Ӳ�֧�֡��������������а��ֲ�����ķ�����ȡ8�˲μ�������֤�ᣬ�ִ���8���������2��.�dz鵽44�����ϵ�����Ϊ![]() �����������
�����������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�ο���ʽ��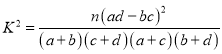 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡���1��������������ܣ���2���ֲ��м�����������Ϊ![]() .
.
��������
(1)��ͳ��������д������������۲�ֵ�������ٽ�ֵ�ó�����;(2)��������֪X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д���������X�ķֲ��У�������ѧ����ֵ.
��1����ͳ����������![]() �������£�
�������£�
44������ | 44�꼰44������ | �ܼ� | |
֧�� | 35 | 45 | 80 |
��֧�� | 15 | 5 | 20 |
�ܼ� | 50 | 50 | 100 |
����۲�ֵ![]() ��
��
�����ڷ�����ĸ��ʲ�����5%��ǰ������Ϊ��44��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��������������ߡ���֧�ֶ��в��죻
��2���������֪��ȡ����8���У�44�����µ���6�ˣ�44�����ϵ���2�ˣ�
�������⣬![]() �Ŀ���ȡֵ��0��1��2��
�Ŀ���ȡֵ��0��1��2��
![]() ��
��
![]() ��
��
![]() ��
��
�ɵ��������X�ķֲ���Ϊ��
| 0 | 1 | 2 |
|
|
|
|
����ѧ����Ϊ![]() .
.

����Ŀ��2016�괺���ڼ�ȫ����������Ⱥ���������ּ���ij�˽�688Ԫ�����������50�����������������Ƶ���ֲ������£�
������ |
|
|
|
|
|
|
Ƶ �� | 3 | 9 | 17 | 11 | 8 | 2 |
��1�����������������Ľ�С��9Ԫ��Ƶ�ʣ�
��2�����������������ƽ����(ͬһ���е������ø���������е�ֵ������)��
��3������50�������ɵ������У���Ƶ����Ϊ���ʣ�
����������������![]() ��Ϊ��������֣������ú����ij��ǡ������������ֵĸ��ʣ�
��Ϊ��������֣������ú����ij��ǡ������������ֵĸ��ʣ�
�������ȡ������������![]() �ڵ����������ߣ������������ֱ�Ϊ
�ڵ����������ߣ������������ֱ�Ϊ![]() ��
��![]() �����¼���
�����¼���![]() ���ĸ��ʣ�
���ĸ��ʣ�
����Ŀ�������Ǽ�������IJ���.16����ʱ��Ϊ�˼���ֵ���㣬��ѧ��ϣ�����˳������Ϊ�ļӼ���.��ʱ�Ѿ�����ѧ�ҷ�������ijЩ������ǿ���ʵ�ֵ�.
���磬��������2�Ĵ��ݵĶ�Ӧ�����Է�������![]() ��ֵ.
��ֵ.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
���ȣ��ڵڶ����ҵ�16��256��Ȼ���ҳ������ڵ�һ�ж�Ӧ��������4��8���������ǵĺͣ���12������ڵ�һ�����ҵ�12���������Ӧ�ĵڶ����е���4096�������![]() ��ֵ.
��ֵ.
�����Ƶķ����������![]() ��ֵ�����ȣ��ڵڶ����ҵ�4096��128��Ȼ���ҳ������ڵ�һ�ж�Ӧ��������12��7���������ǵ�______������ڵ�һ�����ҵ�______���������Ӧ�ĵڶ����е���______�������
��ֵ�����ȣ��ڵڶ����ҵ�4096��128��Ȼ���ҳ������ڵ�һ�ж�Ӧ��������12��7���������ǵ�______������ڵ�һ�����ҵ�______���������Ӧ�ĵڶ����е���______�������![]() ֵ.
ֵ.