题目内容
单调函数f(x)满足f(x + y)= f(x) + f(y),且f(1)=2,其定义域为R。
(1)求f(0)、f(2)、f(4)的值; (2)解不等式f(x2+ 3 x) < 8。
(1)求f(0)、f(2)、f(4)的值; (2)解不等式f(x2+ 3 x) < 8。
(Ⅰ)f(0)="0" f(2)=4 f(4)="8 " (Ⅱ) -4< x <1
(1)令x =1,y =0,得f(0)=0
x =1,y =1,得f(2)=4
x =2,y =2,得f(4)=8
(2)∵函数f(x)为单调函数,且f(4)> f(2),∴f(x)为单调递增函数,
∴只有一个x = 4使得f(x)=8。
∴f(x2+ 3 x) < 8= f(4)
而f(x)为单调递增函数,∴x2+ 3 x<4
∴-4< x <1
x =1,y =1,得f(2)=4
x =2,y =2,得f(4)=8
(2)∵函数f(x)为单调函数,且f(4)> f(2),∴f(x)为单调递增函数,
∴只有一个x = 4使得f(x)=8。
∴f(x2+ 3 x) < 8= f(4)
而f(x)为单调递增函数,∴x2+ 3 x<4
∴-4< x <1

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
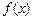 的定义域为R, 对任意实数
的定义域为R, 对任意实数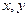 都有
都有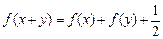 ,
, 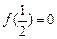 , 当
, 当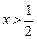 时,
时,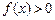 .
.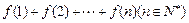 ;
;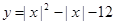 两个零点的差的绝对值是( ).
两个零点的差的绝对值是( ).

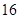
 是奇函数,它们的定域
是奇函数,它们的定域 ,且它们在
,且它们在 上的图象如图所示,则不等式
上的图象如图所示,则不等式 的解集是 .
的解集是 .

 在区间
在区间 是增函数,则常数a的取值范围是
是增函数,则常数a的取值范围是 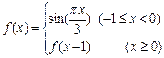 ,则
,则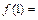 ________________.
________________. ,则
,则 ____
____ 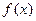 (x∈R)为奇函数,
(x∈R)为奇函数,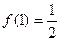 ,
,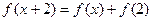 ,则
,则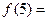 ( )
( ) ;
;