题目内容
(本小题满分12分)
已知函数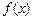 的定义域为R, 对任意实数
的定义域为R, 对任意实数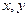 都有
都有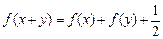 ,
,
且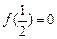 , 当
, 当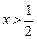 时,
时,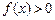 .
.
(1) 求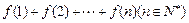 ;
;
(2) 判断函数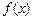 的单调性并证明.
的单调性并证明.
已知函数
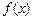 的定义域为R, 对任意实数
的定义域为R, 对任意实数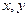 都有
都有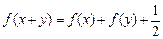 ,
, 且
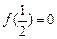 , 当
, 当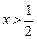 时,
时,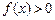 .
.(1) 求
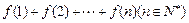 ;
;(2) 判断函数
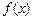 的单调性并证明.
的单调性并证明.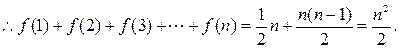
解: (1) 令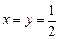 ,则
,则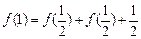 ,
, 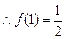 ,
,
则当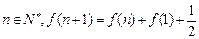 , ∴
, ∴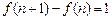 ,
,
∴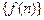 是首项为
是首项为 , 公差为1的等差数列.
, 公差为1的等差数列.
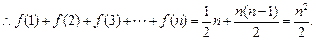
(2)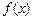 在
在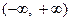 上是增函数.
上是增函数.
证明: 设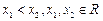 ,
,
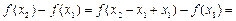
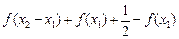
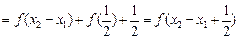 ,
,
∵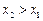 , ∴
, ∴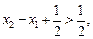 由于当
由于当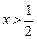 时,
时, 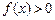 ,
,

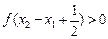 ,即
,即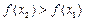 , ∴
, ∴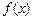 在
在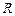 上是增函数.
上是增函数.
【说明】湖北省黄冈中学2009届高三2月月考数学试题(理)
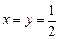 ,则
,则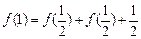 ,
, 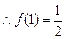 ,
,则当
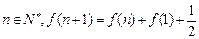 , ∴
, ∴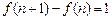 ,
,∴
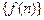 是首项为
是首项为 , 公差为1的等差数列.
, 公差为1的等差数列.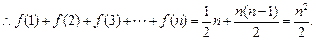
(2)
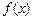 在
在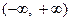 上是增函数.
上是增函数.证明: 设
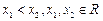 ,
,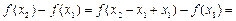
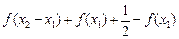
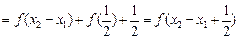 ,
,∵
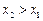 , ∴
, ∴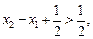 由于当
由于当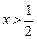 时,
时, 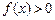 ,
,
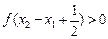 ,即
,即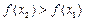 , ∴
, ∴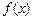 在
在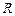 上是增函数.
上是增函数.【说明】湖北省黄冈中学2009届高三2月月考数学试题(理)


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
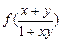 ; ②当x∈(-1,0),f (x) > 0.
; ②当x∈(-1,0),f (x) > 0. 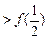 .
. ,
, ,解不等式
,解不等式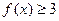 ; (2)如果
; (2)如果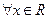 ,
,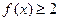 ,求a的取值范围
,求a的取值范围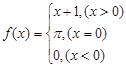 ,则
,则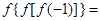 ( ).
( ).



 对于一切实数
对于一切实数 均有
均有 成立,且
成立,且 ,则当
,则当 时,不等式
时,不等式 恒成立时,实数
恒成立时,实数 的取值范围是 ▲ .
的取值范围是 ▲ .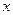 ,符号[
,符号[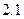 ]=2;[
]=2;[ ]=
]= , 这个函数[
, 这个函数[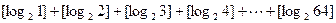 的值为
的值为 ,则
,则 。
。