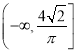题目内容
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
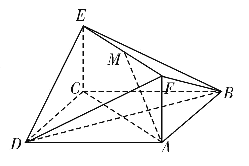
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
试题(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(3)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(I)记![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,∵
,∵![]() 、
、![]() 分别是
分别是
![]() 的中点,
的中点,![]() 是矩形
是矩形
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ∥
∥![]() ,∵
,∵![]() 平面
平面![]()
![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() 6分
6分
(Ⅱ)在平面![]() 中过
中过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]()
∴![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 在平面
在平面![]() 上的射影,
上的射影,
由三垂线定理点得![]()
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,
∴![]()
二面角![]() 的大小为
的大小为![]() 8分
8分
另解:以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,则
,则![]()
(I)易得:![]() ,
,![]()
则![]() ∥
∥![]() ,由
,由![]() 面
面![]() ,故
,故![]() ∥面
∥面![]() ;
;
(Ⅱ)取面![]() 的一个法向量为
的一个法向量为![]() ,面
,面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
故二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】随机调查![]() 名性别不同的大学生是否喜欢打羽毛球,得到如下
名性别不同的大学生是否喜欢打羽毛球,得到如下![]() 列联表:
列联表:
男 | 女 | 总计 | |
喜欢打羽毛球 |
|
|
|
不喜欢打羽毛球 |
|
|
|
总计 |
|
|
|
临界值表:
|
|
|
|
|
|
|
|
参考公式:![]() (其中
(其中![]() )
)
参照临界值表,下列结论正确的是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”
C. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
D. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”