题目内容
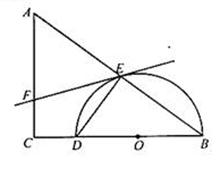
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.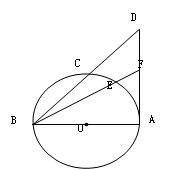

连接CE,过B作⊙O的切线BG,则BG∥AD
∴∠GBC=∠FDB,又∠GBC=∠CEB ∴∠CEB=∠FDB-----------5分
又∠CBE是△BCE和△BDF的公共角 ∴△BCE∽△BDF ∴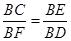 ,
,
即BE•BF=BC•BD…………10分
证法二:连接AC、AE,∵AB是直径,AC是切线 ∴AB⊥AD,AC⊥BD,∠CEB=∠CAB
∵在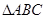 中,∠CAB=
中,∠CAB=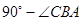 ,在
,在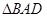 中,∠D=
中,∠D=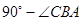
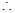 ∠CAB=∠D,
∠CAB=∠D, 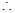 ∠CEB=∠D----------------5分
∠CEB=∠D----------------5分
 C,E,F,D四点共圆
C,E,F,D四点共圆 ∴BE•BF=BC•BD…………10分
∴BE•BF=BC•BD…………10分
证法三:连接AC、AE,∵AB是直径,AC是切线 ∴AB⊥AD,AC⊥BD,AE⊥BF------3分
由射线定理有AB2=BC•BD,AB2=BE•BF-------9分 ∴BE•BF=BC•BD
∴∠GBC=∠FDB,又∠GBC=∠CEB ∴∠CEB=∠FDB-----------5分
又∠CBE是△BCE和△BDF的公共角 ∴△BCE∽△BDF ∴
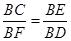 ,
,即BE•BF=BC•BD…………10分
证法二:连接AC、AE,∵AB是直径,AC是切线 ∴AB⊥AD,AC⊥BD,∠CEB=∠CAB
∵在
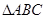 中,∠CAB=
中,∠CAB=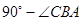 ,在
,在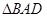 中,∠D=
中,∠D=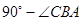
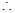 ∠CAB=∠D,
∠CAB=∠D, 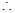 ∠CEB=∠D----------------5分
∠CEB=∠D----------------5分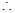 C,E,F,D四点共圆
C,E,F,D四点共圆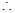 ∴BE•BF=BC•BD…………10分
∴BE•BF=BC•BD…………10分证法三:连接AC、AE,∵AB是直径,AC是切线 ∴AB⊥AD,AC⊥BD,AE⊥BF------3分
由射线定理有AB2=BC•BD,AB2=BE•BF-------9分 ∴BE•BF=BC•BD
采用分析法找到解题途径: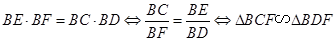
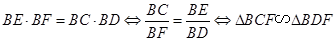

练习册系列答案
相关题目
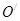 相交于
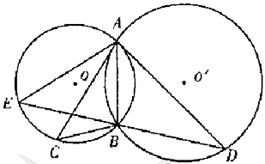
相交于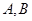 两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E。证明
两点,过A作两圆的切线分别交两圆于C,D两点,连接DB并延长交⊙O于点E。证明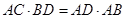 ;
;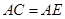 。
。
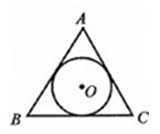
 上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .
上的点(不与点A、C重合),延长BD至E,延长交BC的延长线于F .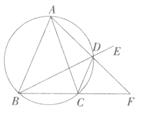
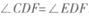 ;
;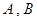 是圆
是圆 上的两点,且
上的两点,且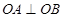 ,
,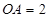 ,
,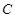 为
为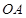 的中点,连接
的中点,连接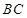 并延长交圆
并延长交圆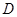 ,则
,则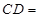 .
.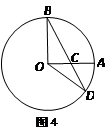
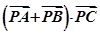 的最小值为 .
的最小值为 .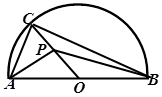
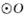 的弦,C、F是
的弦,C、F是 上的点,OC垂直于弦AB,过点F作
上的点,OC垂直于弦AB,过点F作 的切线,交AB的延长线于D,连结CF交AB于点E.
的切线,交AB的延长线于D,连结CF交AB于点E.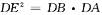 ;
;
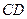 是圆
是圆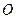 的切线, 切点为
的切线, 切点为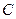 , 点
, 点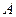 、
、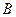 在圆
在圆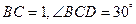 ,则圆
,则圆