题目内容
(本小题满分12分) 已知向量
 ,
, ,
, .
.(1)若
 求向量
求向量 与
与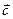 的夹角;
的夹角;(2)当
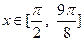 时,求函数
时,求函数 的最大值。
的最大值。解:(1)当x = 时,
cos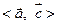 = = = -cosx=-cos = cos。
= = = -cosx=-cos = cos。
∵ 0≤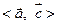 ≤π,∴
≤π,∴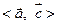 =; …………………………………… 6分
=; …………………………………… 6分
(2) f(x)=2a·b+1=2(-cos2x+sinxcosx)+1=2sinxcosx-(2cos2x-1)
=sin2x-cos2x=sin(2x-)。 ………………………………… 9分
∵ x∈[,],∴2x - ∈[,2π],
故sin(2x-)∈[-1,],
∴当2x-= ,即x=时,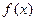 取得最大值,且f(x)max=
取得最大值,且f(x)max=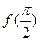 =1。…… 12分
=1。…… 12分
cos
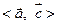 = = = -cosx=-cos = cos。
= = = -cosx=-cos = cos。∵ 0≤
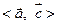 ≤π,∴
≤π,∴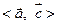 =; …………………………………… 6分
=; …………………………………… 6分(2) f(x)=2a·b+1=2(-cos2x+sinxcosx)+1=2sinxcosx-(2cos2x-1)
=sin2x-cos2x=sin(2x-)。 ………………………………… 9分
∵ x∈[,],∴2x - ∈[,2π],
故sin(2x-)∈[-1,],
∴当2x-= ,即x=时,
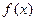 取得最大值,且f(x)max=
取得最大值,且f(x)max=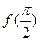 =1。…… 12分
=1。…… 12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. ;
;  是第三象限角,且
是第三象限角,且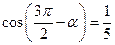 ,求
,求 与
与 的解集分别为
的解集分别为 和
和 ,则( )
,则( )
 与直线
与直线 相交,
相交, 轴右侧的交点自左向右依次记为
轴右侧的交点自左向右依次记为 …,则|
…,则| |等于
|等于 B.
B.  B.
B. D.
D.
 与
与 共线,其中A是△ABC的内角.
共线,其中A是△ABC的内角.
 )且f(x0)=
)且f(x0)= 时,求f(x0+
时,求f(x0+ )的值.
)的值. ,则
,则 ( )
( ) 的偶函数
的偶函数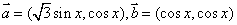 ,
, (
( ).
). 的单调递增区间;
的单调递增区间; 时,
时,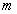 的值.
的值. sinxcosx-1(x∈R)的最大值为M,最小正周期为T.
sinxcosx-1(x∈R)的最大值为M,最小正周期为T.