题目内容
10．复数z1，z2满足|z1|=|z2|=1，|z1+z2|=$\sqrt{3}$，则|z1-z2|=（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
分析 直接利用是的几何意义，判断复数的特征，然后求解即可．
解答 解：根据复数的几何意义，由题意复数z1，z2满足|z1|=|z2|=1，|z1+z2|=$\sqrt{3}$，可将z1，z2看作夹角为60°的单位向量，从而|z1-z2|=1，
故选A．
点评 本小题主要考查复数的几何意义．考查逻辑推理与计算能力．
练习册系列答案
相关题目
如图，已知三棱柱ABC-A1B1C1中，底面ABC是等边三角形，侧棱与底面垂直，点E，F分别为棱BB1，AC中点．
如图，在三棱锥P-ABC中，底面△ABC是边长为2的等边三角形，∠PCA=90°，E，F分别为AP，AC的中点，且PA=4，$BE=\sqrt{3}$．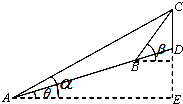
如图，一山顶有一信号塔CD（CD所在的直线与地平面垂直），在山脚A处测得塔尖C的仰角为α，沿倾斜角为θ的山坡向上前进l米后到达B处，测得C的仰角为β．
15．从点P出发的三条射线PA，PB，PC两两成60°角，且分别与球O相切于A，B，C三点，若OP=$\sqrt{3}$，则球的体积为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{4π}{3}$ | D． | $\frac{8π}{3}$ |