题目内容
4.以下四个命题中,正确的是( )| A. | 在定义域内,只有终边相同的角的三角函数值才相等 | |
| B. | {α|α=k+$\frac{π}{6}$,k∈Z}≠{β|β=-k+$\frac{π}{6}$,k∈Z} | |
| C. | 若α是第二象限的角,则sin2α<0 | |
| D. | 第四象限的角可表示为{α|2k+$\frac{3}{2}$<α<2k,k∈Z} |
分析 A,可举例说明命题错误;
B,k∈Z时,{α|α=k+$\frac{π}{6}$}={β|β=-k+$\frac{π}{6}$};
C,α是第二象限的角时,2α是第3、4象限或y负半轴的角,sin2α<0;
D,写出第四象限角所表示的集合.
解答 解:对于A,如sin$\frac{π}{3}$=sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,但$\frac{π}{3}$与$\frac{2π}{3}$的终边不同,∴A错误;
对于B,当k∈Z时,{α|α=k+$\frac{π}{6}$}={β|β=-k+$\frac{π}{6}$},∴B错误;
对于C,当α是第二象限的角时,$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z,
∴π+4kπ<2α<2π+4kπ,k∈Z,∴sin2α<0,C正确;
对于D,第四象限的角应表示为{α|2k+$\frac{3}{2}$π<α<2kπ+2π,k∈Z},∴D错误.
故选:C.
点评 本题考查了终边相同的角,象限角以及终边在坐标轴上的角的坐标表示,也考查了三角函数值符号的判断问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知集合P={1,m},Q={1,3,5},则“m=5”是“P⊆Q”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.某省气象部门为了有效缓解近期的持续高温天气,拟进行人工降雨,为了达到理想效果,首先在电脑上进行人工降雨模拟试验,准备用A,B,C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下:
假设甲、乙、丙三地实施的人工降雨彼此互不影响.
(Ⅰ)求甲、乙两地恰为中雨且丙为小雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲恰需中雨即能达到理想状态,乙必须是大雨才能达到理想状态,丙是小雨或中雨就能达到理想状态,求降雨量达到理想状态的地方个数的概率分布与期望.
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟试验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
(Ⅰ)求甲、乙两地恰为中雨且丙为小雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲恰需中雨即能达到理想状态,乙必须是大雨才能达到理想状态,丙是小雨或中雨就能达到理想状态,求降雨量达到理想状态的地方个数的概率分布与期望.
9.已知变量x,y满足的不等式组$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}\right.$表示的区域为D,B,C为区域D内的任意两点,设$\overrightarrow{OB}$,$\overrightarrow{OC}$的夹角为θ,则tanθ的最大值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
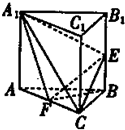 如图,已知三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧棱与底面垂直,点E,F分别为棱BB1,AC中点.
如图,已知三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧棱与底面垂直,点E,F分别为棱BB1,AC中点.