Question

【题目】如图，在平面直角坐标系xOy中，椭圆C： =1（a＞b＞0）的离心率为 ，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切．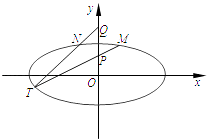

（1）求椭圆C的方程；
（2）已知点P（0，1），Q（0，2）．设M，N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上．

Answer 1

【答案】
（1）解：由题意，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切，∴b= = ．

因为离心率e= = ，所以 = ，所以a=2 ．

所以椭圆C的方程为

（2）证明：由题意可设M，N的坐标分别为（x0，y0），（﹣x0，y0），则直线PM的方程为y= x+1，①

直线QN的方程为y= x+2． ②

设T（x，y），联立①②解得x0= ，y0= ．

因为 ，所以 （ ）2+ （ ）2=1．

整理得 =（2y﹣3）2，所以 ﹣12y+8=4y2﹣12y+9，即 ．

所以点T坐标满足椭圆C的方程，即点T在椭圆C上

【解析】（1）利用以原点为圆心，椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切，可得b的值，利用离心率为 ，即可求得椭圆C的方程；（2）设M，N的坐标分别为（x0 ， y0），（﹣x0 ， y0），求出直线PM、QN的方程，求得x0 ， y0的值，代入椭圆方程，整理可得结论．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：，焦点在y轴：即可以解答此题．