题目内容
【题目】如图,设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点. 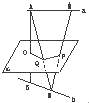
【答案】证明:连接AN,交平面α于点Q,连接PQ.
∵b∥α,b平面ABN,平面ABN∩α=OQ,
∴b∥OQ.又O为AB的中点,
∴Q为AN的中点.∵a∥α,a平面AMN且平面AMN∩α=PQ,
∴a∥PQ.∴P为MN的中点.
【解析】先连接AN,交平面α于点Q,连接PQ,由于b∥α,b平面ABN,平面ABN∩α=OQ,根据线面平行的性质定理可知b∥OQ,同理可证得a∥PQ,从而确定点P的位置.
【考点精析】利用直线与平面平行的性质对题目进行判断即可得到答案,需要熟知一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行.

练习册系列答案
相关题目