题目内容
已知 在区间
在区间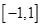 上是增函数.
上是增函数.
(1)求实数 的值组成的集合
的值组成的集合 ;
;
(2)设关于 的方程
的方程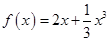 的两个非零实根为
的两个非零实根为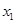 、
、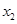 .试问:是否存在实数
.试问:是否存在实数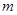 ,使得不等式
,使得不等式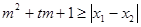 对任意
对任意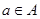 及
及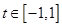 恒成立?若存在,求
恒成立?若存在,求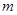 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)实数a的值组成的集合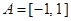 ;
;
(2)存在实数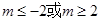 ,使得不等式
,使得不等式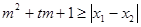 对任意
对任意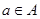 及
及 恒成立.
恒成立.
解析试题分析:(1)先求出函数 的导数
的导数 ,将条件
,将条件 在区间
在区间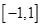 上为增函数这一条件转化为
上为增函数这一条件转化为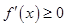 在区间
在区间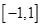 上恒成立,结合二次函数的图象得到
上恒成立,结合二次函数的图象得到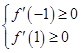 ,从而解出实数
,从而解出实数 的取值范围;(2)先将方程
的取值范围;(2)先将方程 转化为一元二次方程,结合韦达定理得到
转化为一元二次方程,结合韦达定理得到 与
与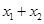 ,然后利用
,然后利用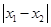
 将
将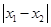 用参数
用参数 进行表示,进而得到不等式
进行表示,进而得到不等式 对任意
对任意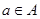
及 恒成立,等价转化为
恒成立,等价转化为 对任意
对任意 恒成立,将不等式
恒成立,将不等式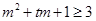 转化为以
转化为以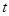 为自变量的一次函数不等式恒成立,只需考虑相应的端点值即可,从而解出参数
为自变量的一次函数不等式恒成立,只需考虑相应的端点值即可,从而解出参数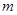 的取值范围.
的取值范围.
试题解析:(1)因为 在区间
在区间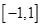 上是增函数,
上是增函数,
所以,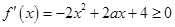 在区间
在区间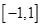 上恒成立,
上恒成立,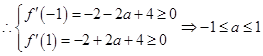 ,
,
所以,实数 的值组成的集合
的值组成的集合 ;
;
(2)由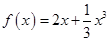 得
得 ,即
,即 ,
,
因为方程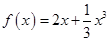 ,即
,即 的两个非零实根为
的两个非零实根为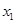 、
、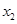 ,
, 、
、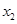 是方程
是方程 两个非零实根,于是
两个非零实根,于是 ,
, ,
,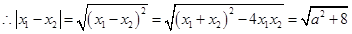 ,
, ,
, ,
,
设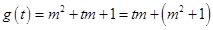 ,
,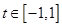 ,
,
则 ,
,
若 对任意
对任意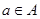 及
及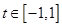 恒成立,
恒成立,
则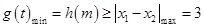 ,解得
,解得 或
或 ,
,
因此,存在实数 或
或 ,使得不等式
,使得不等式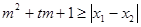 对任意
对任意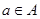 及
及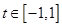 恒成立.
恒成立.
考点:1.函数的单调性;2.二次函数的零点分布;3.韦达定理;4.主次元交换

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量,并求
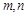 的值.
的值.  .
. 在
在 上为增函数, 求实数
上为增函数, 求实数 的取值范围;
的取值范围; 且
且 时,
时, .
.  对任意
对任意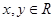 ,都有
,都有 ,当
,当 时,
时,
 时
时  ,
,
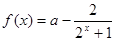 ,
,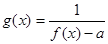 若函数
若函数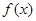 为奇函数,求
为奇函数,求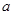 的值.
的值.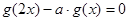 ,有唯一实数解,求
,有唯一实数解,求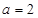 ,则是否存在实数
,则是否存在实数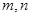
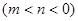 ,使得函数
,使得函数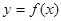 的定义域和值域都为
的定义域和值域都为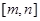 。若存在,求出
。若存在,求出 ,
,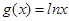 .
. 在
在 上是单调减函数,求
上是单调减函数,求 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 是实数,
是实数,
 成立;
成立; 均为增函数
均为增函数 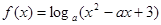
 的值域为
的值域为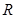 ,求实数
,求实数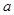 的取值范围;
的取值范围;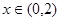 时,函数
时,函数 是定义在
是定义在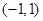 上的奇函数,且
上的奇函数,且 .
.