题目内容
已知 是定义在
是定义在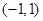 上的奇函数,且
上的奇函数,且 在
在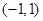 上是减函数,解不等式
上是减函数,解不等式 .
.
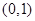 .
.
解析试题分析:不等式 变形为
变形为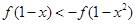 ,然后利用奇函数的定义变为
,然后利用奇函数的定义变为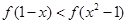 ,再利用函数的单调性,得到关于
,再利用函数的单调性,得到关于 的不等式
的不等式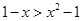 ,同时要注意定义域的限制.这是这一类型问题的通常解法,容易出错的是解题中不考虑定义域,从而得出错误结论.
,同时要注意定义域的限制.这是这一类型问题的通常解法,容易出错的是解题中不考虑定义域,从而得出错误结论.
试题解析:解 ∵ 是定义在
是定义在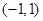 上的奇函数,
上的奇函数,
∴由 ,
,
得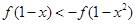 .
.
∴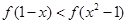 .又∵
.又∵ 在
在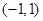 上是减函数,
上是减函数,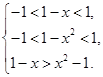
∴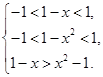 解得
解得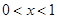 .
.
∴原不等式的解集为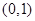 .
.
考点:奇函数与减函数的概念.

练习册系列答案
相关题目
题目内容
已知 是定义在
是定义在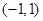 上的奇函数,且
上的奇函数,且 在
在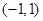 上是减函数,解不等式
上是减函数,解不等式 .
.
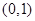 .
.
解析试题分析:不等式 变形为
变形为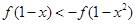 ,然后利用奇函数的定义变为
,然后利用奇函数的定义变为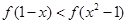 ,再利用函数的单调性,得到关于
,再利用函数的单调性,得到关于 的不等式
的不等式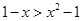 ,同时要注意定义域的限制.这是这一类型问题的通常解法,容易出错的是解题中不考虑定义域,从而得出错误结论.
,同时要注意定义域的限制.这是这一类型问题的通常解法,容易出错的是解题中不考虑定义域,从而得出错误结论.
试题解析:解 ∵ 是定义在
是定义在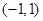 上的奇函数,
上的奇函数,
∴由 ,
,
得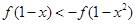 .
.
∴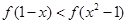 .又∵
.又∵ 在
在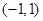 上是减函数,
上是减函数,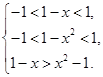
∴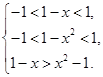 解得
解得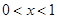 .
.
∴原不等式的解集为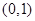 .
.
考点:奇函数与减函数的概念.
