题目内容
已知函数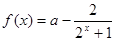 ,
,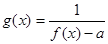 若函数
若函数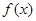 为奇函数,求
为奇函数,求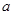 的值.
的值.
(2)若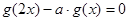 ,有唯一实数解,求
,有唯一实数解,求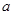 的取值范围.
的取值范围.
(3)若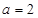 ,则是否存在实数
,则是否存在实数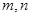
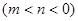 ,使得函数
,使得函数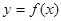 的定义域和值域都为
的定义域和值域都为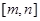 。若存在,求出
。若存在,求出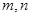 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)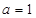 ;(2)
;(2)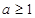 ;(3)不存在实数
;(3)不存在实数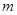 、
、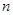 满足题意.
满足题意.
解析试题分析:(1)由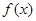 是定义在
是定义在 上的奇函数,可知
上的奇函数,可知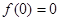 ,从中求出
,从中求出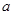 的值;(2)将原不等式化简,最后可将问题转化为方程
的值;(2)将原不等式化简,最后可将问题转化为方程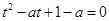 在
在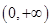 上有唯一解,令
上有唯一解,令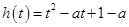 ,则
,则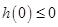
从而求出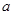 的取值范围;(3)由函数
的取值范围;(3)由函数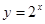 在
在 上是增函数,可得到
上是增函数,可得到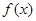 在
在 上是增函数,假设存在
上是增函数,假设存在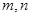
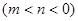 ,使得函数
,使得函数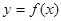 的定义域和值域都为
的定义域和值域都为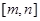 ,则
,则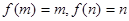 ,而这两个等式都无解,所以不存在
,而这两个等式都无解,所以不存在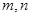 满足题意.
满足题意.
试题解析:
(1)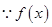 为奇函数
为奇函数 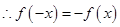
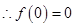
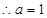
(2)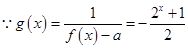
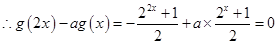
令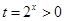 ,则问题转化为方程
,则问题转化为方程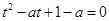 在
在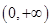 上有唯一解.
上有唯一解.
令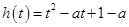 ,则
,则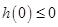
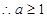
(3)不存在实数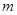 、
、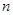 满足题意,
满足题意,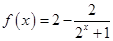
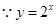 在
在 上是增函数
上是增函数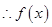 在
在 上是增函数
上是增函数
假设存在实数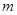 、
、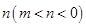 满足题意,有
满足题意,有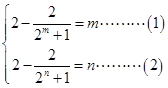
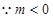
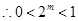

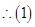 式左边
式左边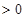 ,右边
,右边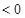 ,故
,故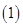 式无解.
式无解.
同理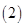 式无解.
式无解.
故不存在实数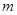 、
、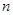 满足题意.
满足题意.
考点:本题考查了函数的奇偶性,单调性以及函数的定义域和值域之间的关系,同时也考查了函数和方程的数学思想,是一道综合题,难度适中.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数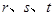 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形. .
. .
. 时,指出
时,指出 的单调递减区间和奇偶性(不需说明理由);
的单调递减区间和奇偶性(不需说明理由); 的零点;
的零点; 不等式
不等式 恒成立,求实数
恒成立,求实数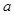 的取值范围。
的取值范围。 且
且 ,函数
,函数 ,
, ,记
,记 .
. 的定义域
的定义域 及其零点;
及其零点; 的方程
的方程 在区间
在区间 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围. 在区间
在区间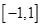 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程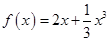 的两个非零实根为
的两个非零实根为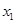 、
、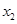 .试问:是否存在实数
.试问:是否存在实数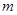 ,使得不等式
,使得不等式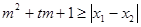 对任意
对任意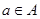 及
及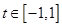 恒成立?若存在,求
恒成立?若存在,求 与时刻x的关系为
与时刻x的关系为 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且 ,若用每天
,若用每天 .
. ,求t的取值范围;
,求t的取值范围; 的最小值为
的最小值为 ,且关于
,且关于 的一元二次不等式
的一元二次不等式 的解集为
的解集为 。
。 的解析式;
的解析式; 其中
其中 ,求函数
,求函数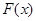 在
在 时的最大值
时的最大值 ;
; (
( 为实数),对任意
为实数),对任意 ,总存在
,总存在 使得
使得 成立,求实数
成立,求实数 是定义在
是定义在 上的增函数,且
上的增函数,且
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
.