题目内容
已知函数 ,
,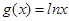 .
.
(1)如果函数 在
在 上是单调减函数,求
上是单调减函数,求 的取值范围;
的取值范围;
(2)是否存在实数 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)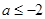 ;(2)存在,且
;(2)存在,且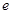 的范围是
的范围是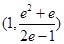 .
.
解析试题分析:(1)由于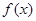 是多项式函数,故对最高次项系数分类,
是多项式函数,故对最高次项系数分类,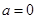 时它是一次函数,是增函数,不是减函数,当
时它是一次函数,是增函数,不是减函数,当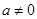 时,
时,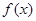 是二次函数,需要考虑对称轴和开口方向;(2)首先把方程
是二次函数,需要考虑对称轴和开口方向;(2)首先把方程 化简,变为
化简,变为 ,设
,设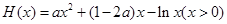 ,即方程
,即方程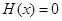 在区间
在区间 内有且只有两个不相等的实数根,转化为讨论函数
内有且只有两个不相等的实数根,转化为讨论函数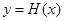 的单调性及极值问题,如本题中,通过分析导函数
的单调性及极值问题,如本题中,通过分析导函数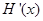 ,知
,知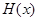 在
在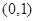 上是减函数,在
上是减函数,在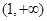 上增函数,因此条件为
上增函数,因此条件为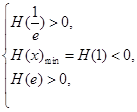 解这个不等式组即得所求
解这个不等式组即得所求 的取值范围.
的取值范围.
试题解析:(1)当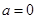 时,
时,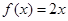 在
在 是单调增函数,不符合题意;
是单调增函数,不符合题意;
当 时,
时, 的对称轴方程为
的对称轴方程为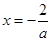 ,由于
,由于 在
在 上是单调增函数,不符合题意;
上是单调增函数,不符合题意;
当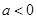 时,函数
时,函数 在
在 上是单调减函数,则
上是单调减函数,则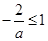 ,解得
,解得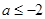 .
.
综上, 的取值范围是
的取值范围是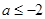 . 4分
. 4分
(2)把方程 整理为
整理为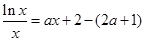 ,
,
即为方程 , 5分
, 5分
设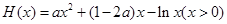 ,原方程在区间
,原方程在区间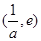 内有且只有两个不相等的实数根,即为函数
内有且只有两个不相等的实数根,即为函数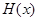 在区间
在区间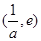 内有且只有两个零点. 6分
内有且只有两个零点. 6分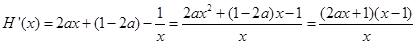 ,
,
令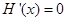 ,∵
,∵ ,解得
,解得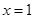 或
或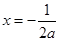 (舍),
(舍),
当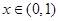 时,
时,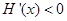 ,
,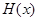 是减函数,
是减函数,
当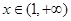 时,
时,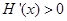 ,
,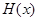 是增函数. 10分
是增函数. 10分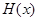 在
在 内有且只有两个不相等的零点,只需
内有且只有两个不相等的零点,只需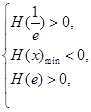 11分
11分
即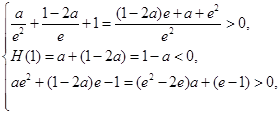 ∴
∴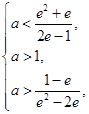
解得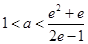 ,所以
,所以 的取值范围是
的取值范围是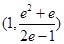 .
.
考点:(1)单调减函数的判定;(2)方程根的个数的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (
( )
) 是定义在R上的偶函数,求a的值;
是定义在R上的偶函数,求a的值; 对任意
对任意 ,
, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.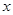 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当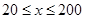 时,车流速度
时,车流速度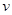 是车流密度x的一次函数.
是车流密度x的一次函数.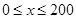 时,求函数
时,求函数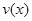 的表达式;
的表达式;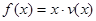 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)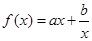 ,且
,且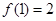 ,
,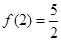 (1)判断函数
(1)判断函数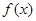 的奇偶性;(2)判断
的奇偶性;(2)判断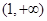 上的单调性并加以证明.
上的单调性并加以证明. 在区间
在区间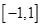 上是增函数.
上是增函数. 的值组成的集合
的值组成的集合 ;
; 的方程
的方程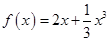 的两个非零实根为
的两个非零实根为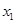 、
、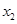 .试问:是否存在实数
.试问:是否存在实数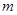 ,使得不等式
,使得不等式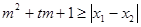 对任意
对任意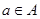 及
及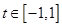 恒成立?若存在,求
恒成立?若存在,求 的定义域为
的定义域为 ,
,  ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.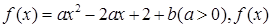 在
在 上最大值是5,最小值是2,若
上最大值是5,最小值是2,若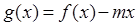 ,在
,在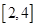 上是单调函数,求m的取值范围.
上是单调函数,求m的取值范围.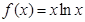 .
. 的单调区间和极值;
的单调区间和极值;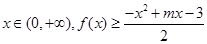 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.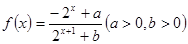 .
.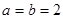 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数; 与
与 的值;
的值;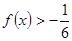 的解集.
的解集.