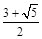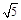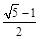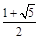题目内容
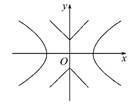
(2013·上海高考)如图,已知双曲线C1: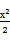 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
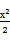 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2=
 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”. (1)x=-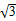 或y=k(x+
或y=k(x+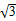 ),其中|k|≥
),其中|k|≥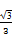 .
.
(2)见解析 (3)见解析
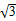 或y=k(x+
或y=k(x+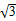 ),其中|k|≥
),其中|k|≥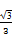 .
.(2)见解析 (3)见解析
(1)C1的左焦点为(-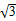 ,0),写出的直线方程可以是以下形式:
,0),写出的直线方程可以是以下形式:
x=-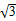 或y=k(x+
或y=k(x+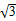 ),其中|k|≥
),其中|k|≥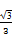 .
.
(2)因为直线y=kx与C2有公共点,
所以方程组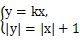 有实数解,
有实数解,
因此|kx|=|x|+1,得|k|=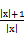 >1.
>1.
若原点是“C1-C2型点”,则存在过原点的直线与C1,C2都有公共点.
考虑过原点与C2有公共点的直线x=0或y=kx(|k|>1).显然直线x=0与C1无公共点.
如果直线为y=kx(|k|>1),
则由方程组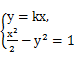 得x2=
得x2=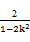 <0,矛盾,
<0,矛盾,
所以直线y=kx(|k|>1)与C1也无公共点.
因此原点不是“C1-C2型点”.
(3)记圆O:x2+y2= ,取圆O内的一点Q,
,取圆O内的一点Q,
设有经过Q的直线l与C1,C2都有公共点,
显然l不垂直于x轴,故可设l:y=kx+b.
若|k|≤1,由于圆O夹在两组平行线y=x±1与y=-x±1之间,
因此圆O也夹在直线y=kx±1与y=-kx±1之间,从而过Q且以k为斜率的直线l与C2无公共点,矛盾,所以|k|>1.
因为l与C1有公共点,所以方程组 有实数解,得(1-2k2)x2-4kbx-2b2-2=0.
有实数解,得(1-2k2)x2-4kbx-2b2-2=0.
因为|k|>1,所以1-2k2≠0,
因此Δ=(4kb)2-4(1-2k2)(-2b2-2)=8(b2+1-2k2)≥0,即b2≥2k2-1.
因为圆O的圆心(0,0)到直线l的距离d=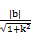 ,
,
所以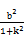 =d2<
=d2< ,从而
,从而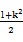 >b2≥2k2-1,
>b2≥2k2-1,
得k2<1,与|k|>1矛盾.
因此,圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
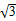 ,0),写出的直线方程可以是以下形式:
,0),写出的直线方程可以是以下形式:x=-
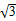 或y=k(x+
或y=k(x+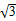 ),其中|k|≥
),其中|k|≥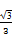 .
.(2)因为直线y=kx与C2有公共点,
所以方程组
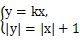 有实数解,
有实数解,因此|kx|=|x|+1,得|k|=
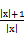 >1.
>1.若原点是“C1-C2型点”,则存在过原点的直线与C1,C2都有公共点.
考虑过原点与C2有公共点的直线x=0或y=kx(|k|>1).显然直线x=0与C1无公共点.
如果直线为y=kx(|k|>1),
则由方程组
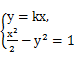 得x2=
得x2=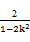 <0,矛盾,
<0,矛盾,所以直线y=kx(|k|>1)与C1也无公共点.
因此原点不是“C1-C2型点”.
(3)记圆O:x2+y2=
 ,取圆O内的一点Q,
,取圆O内的一点Q,设有经过Q的直线l与C1,C2都有公共点,
显然l不垂直于x轴,故可设l:y=kx+b.
若|k|≤1,由于圆O夹在两组平行线y=x±1与y=-x±1之间,
因此圆O也夹在直线y=kx±1与y=-kx±1之间,从而过Q且以k为斜率的直线l与C2无公共点,矛盾,所以|k|>1.
因为l与C1有公共点,所以方程组
 有实数解,得(1-2k2)x2-4kbx-2b2-2=0.
有实数解,得(1-2k2)x2-4kbx-2b2-2=0.因为|k|>1,所以1-2k2≠0,
因此Δ=(4kb)2-4(1-2k2)(-2b2-2)=8(b2+1-2k2)≥0,即b2≥2k2-1.
因为圆O的圆心(0,0)到直线l的距离d=
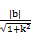 ,
,所以
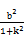 =d2<
=d2< ,从而
,从而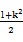 >b2≥2k2-1,
>b2≥2k2-1,得k2<1,与|k|>1矛盾.
因此,圆x2+y2=
 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
练习册系列答案
相关题目
 ,直线
,直线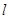 的方程为
的方程为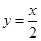 ,点
,点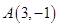 关于直线
关于直线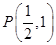 ,点
,点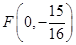 是抛物线的焦点,
是抛物线的焦点,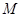 是抛物线上的动点,求
是抛物线上的动点,求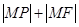 的最小值及此时点
的最小值及此时点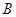 、
、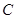 是抛物线上的动点,点
是抛物线上的动点,点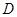 是抛物线与
是抛物线与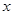 轴正半轴交点,
轴正半轴交点, 是以
是以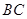 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. 
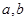 ,定义
,定义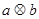 的算法原理如右侧程序框图所示.设
的算法原理如右侧程序框图所示.设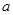 为函数
为函数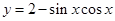 的最大值,
的最大值,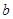 为双曲线
为双曲线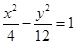 的离心率,则计算机执行该运算后输出的结果是( )
的离心率,则计算机执行该运算后输出的结果是( )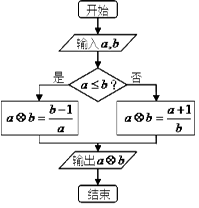
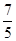
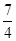
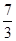
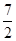
 的焦点为
的焦点为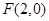 ,则
,则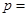 ________,
________, 向其准线作垂线,记与抛物线的交点为
向其准线作垂线,记与抛物线的交点为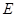 ,则
,则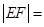 _____.
_____.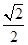 .
.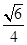 .若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果
.若A、B两点关于x轴对称,E为线段AB的中点,射线OE交椭圆C于点P.如果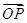 =t
=t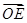 ,求实数t的值.
,求实数t的值.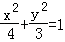 的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[﹣2,﹣1],那么直线PA1斜率的取值范围是( )
的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[﹣2,﹣1],那么直线PA1斜率的取值范围是( )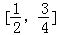
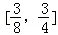
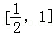
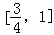
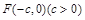 是双曲线
是双曲线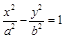 的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆
的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆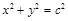 交于点P,且点P在抛物线
交于点P,且点P在抛物线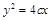 上,则e2 =( )
上,则e2 =( )