题目内容
如图,等腰梯形ABCD中,线段Ab的中点O是抛物线的顶点,DA、AB、BC分别与抛物线切于点M、O、N.等腰梯形的高是3,直线CD与抛物线相交于E、F两点,线段EF的长是4.
(Ⅰ)建立适当的直角坐标系,求抛物线的方程;
(Ⅱ)求等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.
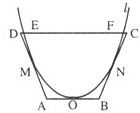
(Ⅰ)建立适当的直角坐标系,求抛物线的方程;
(Ⅱ)求等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.

(Ⅰ)以AB所在直线为x轴,以O为圆点,建立直角坐标系,则F(2,3),
设抛物线方程为y=ax2,a>0,
将F(2,3)代入,得a=
,
所以,抛物线方程为x2=
y,x∈R,
(Ⅱ)由(Ⅰ)知:y=
x2,x∈R,y′=
x,
设N(x0,y0),过点N的切线方程为y-y0=
x0(x-x0),
令y=0,又y0=
x02,∴x=
x0,
∴B(
x0,0).
令y=3,又y0=
x02,∴x=
,
∴C(
,3),
∴S四边形=(
+
)•3=3(
+x0)≥6
,
当且仅当
=x0,即x0=
时,取“=”号,此时N(
,
),M(-
,
).
设抛物线方程为y=ax2,a>0,
将F(2,3)代入,得a=
| 3 |
| 4 |
所以,抛物线方程为x2=
| 4 |
| 3 |
(Ⅱ)由(Ⅰ)知:y=
| 3 |
| 4 |
| 3 |
| 2 |
设N(x0,y0),过点N的切线方程为y-y0=
| 3 |
| 2 |
令y=0,又y0=
| 3 |
| 4 |
| 1 |
| 2 |
∴B(
| 1 |
| 2 |
令y=3,又y0=
| 3 |
| 4 |
| x02+4 |
| 2x0 |
∴C(
| x02+4 |
| 2x0 |
∴S四边形=(
| x0 |
| 2 |
| x02+4 |
| 2x0 |
| 2 |
| x0 |
| 2 |
当且仅当
| 2 |
| x0 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
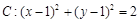 经过椭圆
经过椭圆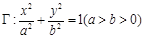 的右焦点
的右焦点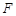 和上顶点
和上顶点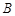 .
. 的方程;
的方程;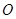 的射线
的射线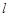 与椭圆
与椭圆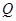 ,与圆
,与圆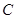 的交点为
的交点为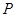 ,
,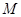 为
为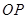 的中点,求
的中点,求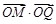 的最大值.
的最大值.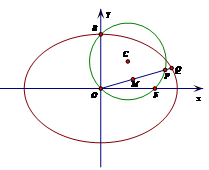
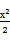 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.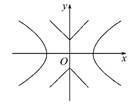
 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”. 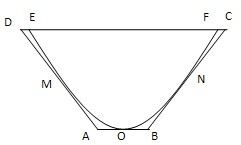
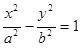
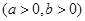 的一个焦点与抛物线
的一个焦点与抛物线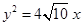 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于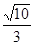 ,则该双曲线的方程为( )
,则该双曲线的方程为( )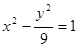
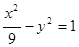
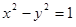
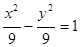
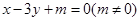 与双曲线
与双曲线 的两条渐近线分别交于
的两条渐近线分别交于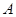 、
、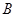 ,若
,若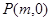 满足
满足 ,则双曲线的离心率是 .
,则双曲线的离心率是 .