题目内容
已知函数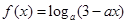 .
.
(1) 当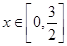 时,函数
时,函数 恒有意义,求实数a的取值范围;
恒有意义,求实数a的取值范围;
(2) 是否存在这样的实数a,使得函数 在区间
在区间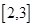 上为增函数,并且
上为增函数,并且 的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
的最大值为1.如果存在,试求出a的值;如果不存在,请说明理由.
(1)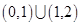 ;(2)存在,
;(2)存在,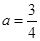 .
.
解析试题分析:(1)首先根据对数函数的底数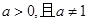 ,得到
,得到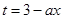 为减函数,最小值是
为减函数,最小值是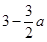 ,再根据对数函数的真数大于0,得到
,再根据对数函数的真数大于0,得到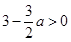 恒成立,在
恒成立,在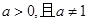 范围内解不等式即可;(2)先看真数部分
范围内解不等式即可;(2)先看真数部分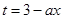 是减函数,由已知“
是减函数,由已知“ 在区间
在区间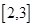 上为增函数”可得,
上为增函数”可得,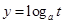 为减函数,此时得到
为减函数,此时得到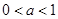 ;根据“
;根据“ 的最大值为1”,结合对数函数的真数大于0,可知
的最大值为1”,结合对数函数的真数大于0,可知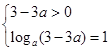 ,解出
,解出 ,再判断它是不是在
,再判断它是不是在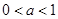 的范围内,在这个范围内,那么得到的
的范围内,在这个范围内,那么得到的 的值满足题目要求,不在这个范围内就说明满足题目要求的
的值满足题目要求,不在这个范围内就说明满足题目要求的 是不存在的.
是不存在的.
试题解析:(1)∵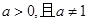 ,设
,设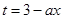 ,
,
则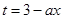 为减函数,
为减函数,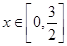 时,t最小值为
时,t最小值为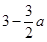 , 2分
, 2分
当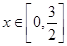 ,
, 恒有意义,即
恒有意义,即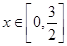 时,
时,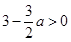 恒成立.即
恒成立.即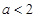 ;4分
;4分
又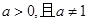 ,∴
,∴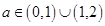 6分
6分
(2)令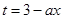 ,则
,则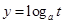 ; ∵
; ∵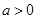 ,∴ 函数
,∴ 函数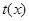 为减函数,
为减函数,
又∵ 在区间
在区间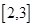 上为增函数,∴
上为增函数,∴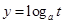 为减函数,∴
为减函数,∴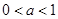 ,8分
,8分
所以 时,
时,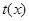 最小值为
最小值为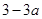 ,此时
,此时 最大值为
最大值为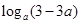 ;9分
;9分
又 的最大值为1,所以
的最大值为1,所以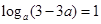 , 10分
, 10分
∴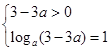 ,即
,即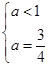 , 所以
, 所以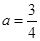 ,故这样的实数a存在. 12分
,故这样的实数a存在. 12分
考点:1.对数函数的定义及定义域;2.对数函数的单调性及其应用;3.对数函数的值域与最值;4.简单复合函数的单调性;5.解不等式

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 毫克)与时间
毫克)与时间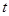 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,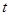 的函数关系式为
的函数关系式为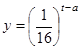 (
(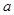 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: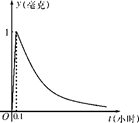
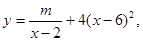 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)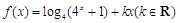 是偶函数.
是偶函数.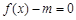 有解,求m的取值范围.
有解,求m的取值范围.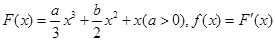 ,若
,若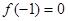 且对任意实数
且对任意实数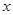 均有
均有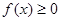 成立.
成立.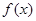 表达式;
表达式;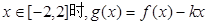 是单调函数,求实数
是单调函数,求实数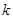 的取值范围.
的取值范围.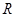 上的函数
上的函数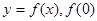
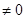 ,当
,当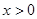 时,
时,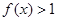 ,且对任意的
,且对任意的 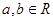 ,有
,有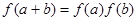 ,
,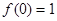 ;
;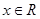 ,恒有
,恒有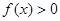 ;
;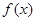 是
是 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式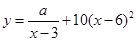 ,其中
,其中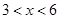 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.