题目内容
(本小题满分16分)设实数a为正数,函数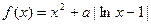 .(Ⅰ)当
.(Ⅰ)当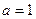 时,求曲线
时,求曲线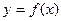 在
在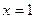 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当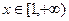 时,求函数
时,求函数 的最小值.
的最小值.
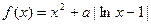 .(Ⅰ)当
.(Ⅰ)当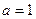 时,求曲线
时,求曲线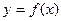 在
在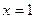 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当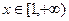 时,求函数
时,求函数 的最小值.
的最小值.(Ⅰ)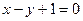 (Ⅱ)
(Ⅱ) 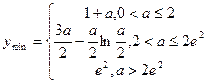
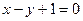 (Ⅱ)
(Ⅱ) 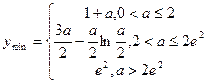
(1)当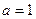 时,
时,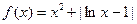
令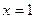 得
得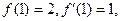 所以切点为(1,2),切线的斜率为1,
所以切点为(1,2),切线的斜率为1,
所以曲线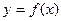 在
在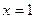 处的切线方程为:
处的切线方程为: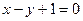 。…4分
。…4分
(2)①当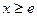 时,
时,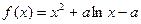 ,
,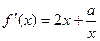
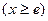
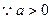 ,
,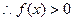 恒成立。
恒成立。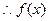 在
在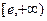 上增函数。故当
上增函数。故当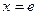 时,
时,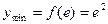
② 当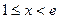 时,
时,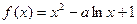 ,
,
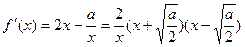 (
(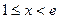 )…………8分
)…………8分
(i)当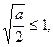 即
即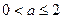 时,
时,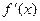 在
在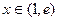 时为正数,所以
时为正数,所以 在区间
在区间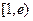 上为增函数。故当
上为增函数。故当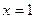 时,
时,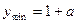 ,且此时
,且此时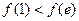
(ii)当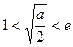 ,即
,即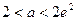 时,
时,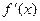 在
在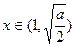 时为负数,在间
时为负数,在间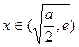 时为正数。所以
时为正数。所以 在区间
在区间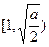 上为减函数,在
上为减函数,在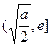 上为增函数
上为增函数
故当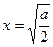 时,
时,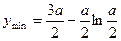 ,且此时
,且此时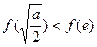 …………10分
…………10分
(iii)当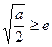 ;即
;即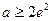 时,
时,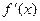 在
在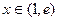 时为负数,所以
时为负数,所以 在区间[1,e]上为减函数,故当
在区间[1,e]上为减函数,故当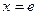 时,
时,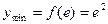 。
。
综上所述,当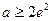 时,
时, 在
在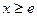 时和
时和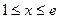 时的最小值都是
时的最小值都是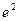 ………12分
………12分
所以此时 的最小值为
的最小值为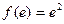 ;当
;当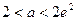 时,
时, 在
在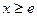 时的最小值为
时的最小值为
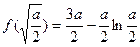 ,而
,而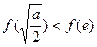 ,所以此时
,所以此时 的最小值为
的最小值为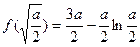 。
。
当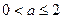 时,在
时,在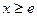 时最小值为
时最小值为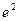 ,在
,在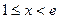 时的最小值为
时的最小值为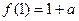
而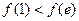 ,所以此时
,所以此时 的最小值为
的最小值为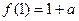
所以函数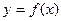 的最小值为
的最小值为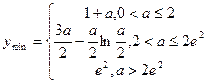 …………16分
…………16分
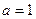 时,
时,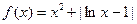
令
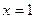 得
得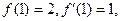 所以切点为(1,2),切线的斜率为1,
所以切点为(1,2),切线的斜率为1,所以曲线
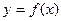 在
在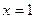 处的切线方程为:
处的切线方程为: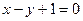 。…4分
。…4分(2)①当
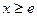 时,
时,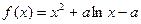 ,
,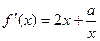
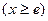
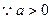 ,
,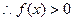 恒成立。
恒成立。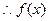 在
在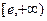 上增函数。故当
上增函数。故当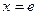 时,
时,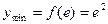
② 当
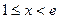 时,
时,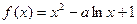 ,
,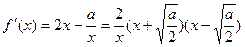 (
(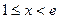 )…………8分
)…………8分(i)当
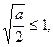 即
即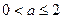 时,
时,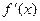 在
在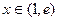 时为正数,所以
时为正数,所以 在区间
在区间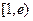 上为增函数。故当
上为增函数。故当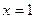 时,
时,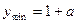 ,且此时
,且此时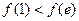
(ii)当
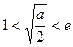 ,即
,即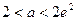 时,
时,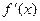 在
在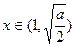 时为负数,在间
时为负数,在间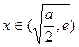 时为正数。所以
时为正数。所以 在区间
在区间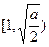 上为减函数,在
上为减函数,在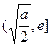 上为增函数
上为增函数故当
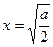 时,
时,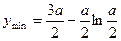 ,且此时
,且此时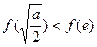 …………10分
…………10分(iii)当
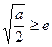 ;即
;即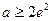 时,
时,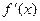 在
在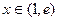 时为负数,所以
时为负数,所以 在区间[1,e]上为减函数,故当
在区间[1,e]上为减函数,故当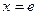 时,
时,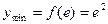 。
。综上所述,当
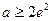 时,
时, 在
在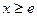 时和
时和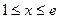 时的最小值都是
时的最小值都是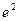 ………12分
………12分所以此时
 的最小值为
的最小值为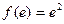 ;当
;当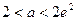 时,
时, 在
在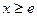 时的最小值为
时的最小值为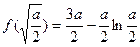 ,而
,而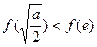 ,所以此时
,所以此时 的最小值为
的最小值为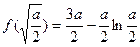 。
。当
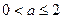 时,在
时,在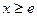 时最小值为
时最小值为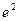 ,在
,在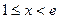 时的最小值为
时的最小值为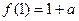
而
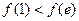 ,所以此时
,所以此时 的最小值为
的最小值为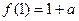
所以函数
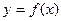 的最小值为
的最小值为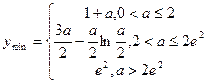 …………16分
…………16分
练习册系列答案
相关题目
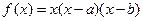 ,点
,点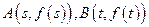 .
.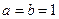 ,求函数
,求函数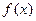 的单调递增区间;
的单调递增区间;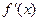 满足:当
满足:当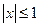 时,有
时,有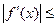
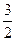 恒成立,求函数
恒成立,求函数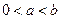 ,函数
,函数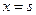 和
和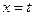 处取得极值,且
处取得极值,且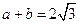 ,证明:
,证明: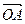 与
与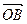 不可能垂直。
不可能垂直。 为常数);
为常数);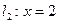 .若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
.若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.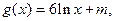 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.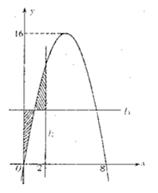
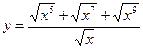
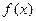 是定义在
是定义在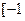 ,
,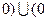 ,
,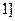 上的奇函数,当
上的奇函数,当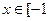 ,
,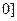 时,
时,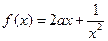 (a为实数).
(a为实数).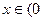 ,
,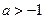 ,试判断
,试判断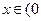 ,
,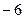 .
.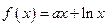 ,
,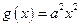 .
.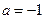 时,求函数
时,求函数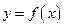 图象上的点到直线
图象上的点到直线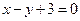 距离的最小值;
距离的最小值;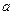 ,使
,使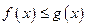 对一切正实数
对一切正实数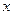 都成立?若存在,求出
都成立?若存在,求出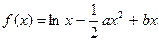
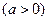 且导数
且导数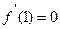 .
.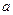 的式子表示
的式子表示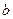 ,并求
,并求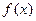 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点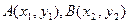 ,如果在函数图象上存在点
,如果在函数图象上存在点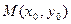 (其中
(其中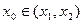 )使得点
)使得点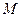 处的切线
处的切线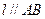 ,则称
,则称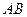 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当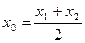 时,又称
时,又称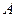 、
、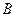 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出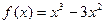 ,给出下列四个命题:①
,给出下列四个命题:①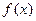 是增函数,无极值;②
是增函数,无极值;②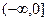 及
及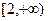 上是增函数;④
上是增函数;④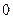 ,极小值
,极小值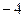 ;其中正确命题的个数为( )
;其中正确命题的个数为( )