题目内容
已知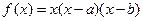 ,点
,点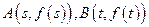 .
.
(Ⅰ)若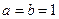 ,求函数
,求函数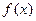 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数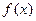 的导函数
的导函数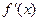 满足:当
满足:当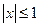 时,有
时,有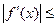
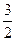 恒成立,求函数
恒成立,求函数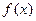 的解析表达式;
的解析表达式;
(Ⅲ)若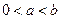 ,函数
,函数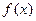 在
在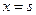 和
和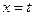 处取得极值,且
处取得极值,且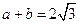 ,证明:
,证明: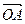 与
与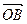 不可能垂直。
不可能垂直。
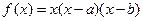 ,点
,点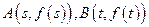 .
.(Ⅰ)若
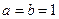 ,求函数
,求函数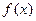 的单调递增区间;
的单调递增区间;(Ⅱ)若函数
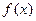 的导函数
的导函数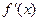 满足:当
满足:当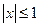 时,有
时,有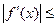
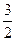 恒成立,求函数
恒成立,求函数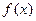 的解析表达式;
的解析表达式;(Ⅲ)若
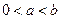 ,函数
,函数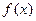 在
在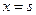 和
和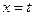 处取得极值,且
处取得极值,且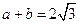 ,证明:
,证明: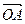 与
与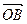 不可能垂直。
不可能垂直。(1)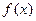 的增区间
的增区间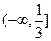 和
和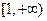 ;(2)
;(2) ;(3)同解析。
;(3)同解析。
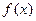 的增区间
的增区间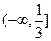 和
和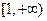 ;(2)
;(2) ;(3)同解析。
;(3)同解析。 (Ⅰ) 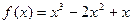 ,
, 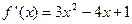
令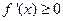 得
得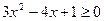 ,解得
,解得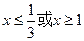
故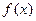 的增区间
的增区间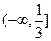 和
和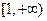
(Ⅱ)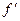 (x)=
(x)=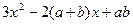
当x∈[-1,1]时,恒有|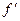 (x)|≤
(x)|≤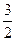 .
.
故有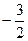 ≤
≤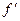 (1)≤
(1)≤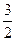 ,
,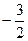 ≤
≤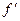 (-1)≤
(-1)≤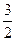 ,
,
及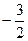 ≤
≤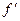 (0)≤
(0)≤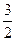 ,
,
即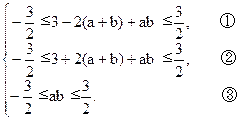
①+②,得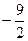 ≤
≤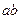 ≤
≤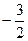 , 又由③,得
, 又由③,得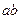 =
=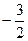 ,将上式代回①和②,得
,将上式代回①和②,得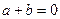 故
故
 .
.
(Ⅲ)假设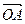 ⊥
⊥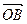 ,即
,即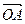
 =
=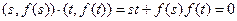
故(s-a)(s-b)(t-a)(t-b)="-1 " [st-(s+t)a+a2][st-(s+t)b+b2]=-1,
由s,t为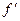 (x)=0的两根可得,s+t=
(x)=0的两根可得,s+t=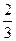 (a+b), st=
(a+b), st=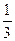
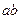 , (0<a<b)
, (0<a<b)
从而有ab(a-b)2=9.
这样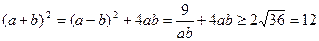
即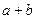 ≥2
≥2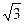 ,这与
,这与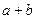 <2
<2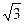 矛盾.
矛盾.
故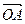 与
与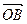 不可能垂直.
不可能垂直.
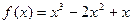 ,
, 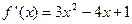
令
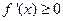 得
得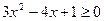 ,解得
,解得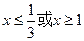
故
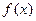 的增区间
的增区间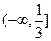 和
和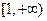
(Ⅱ)
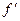 (x)=
(x)=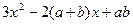
当x∈[-1,1]时,恒有|
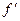 (x)|≤
(x)|≤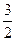 .
. 故有
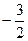 ≤
≤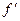 (1)≤
(1)≤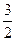 ,
,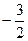 ≤
≤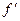 (-1)≤
(-1)≤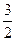 ,
,及
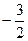 ≤
≤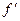 (0)≤
(0)≤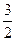 ,
,即
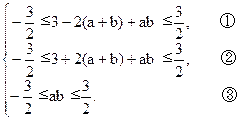
①+②,得
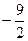 ≤
≤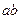 ≤
≤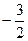 , 又由③,得
, 又由③,得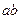 =
=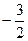 ,将上式代回①和②,得
,将上式代回①和②,得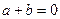 故
故
 .
.(Ⅲ)假设
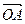 ⊥
⊥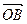 ,即
,即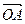
 =
=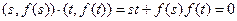
故(s-a)(s-b)(t-a)(t-b)="-1 " [st-(s+t)a+a2][st-(s+t)b+b2]=-1,
由s,t为
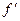 (x)=0的两根可得,s+t=
(x)=0的两根可得,s+t=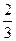 (a+b), st=
(a+b), st=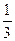
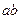 , (0<a<b)
, (0<a<b)从而有ab(a-b)2=9.
这样
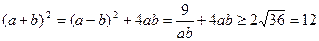
即
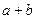 ≥2
≥2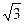 ,这与
,这与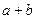 <2
<2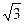 矛盾.
矛盾. 故
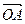 与
与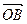 不可能垂直.
不可能垂直. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
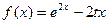 ,
,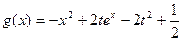 .
.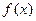 在区间
在区间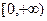 的最小值;(2)求证:若
的最小值;(2)求证:若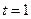 ,则不等式
,则不等式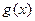 ≥
≥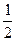 对于任意的
对于任意的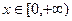 恒成立;(3)求证:若
恒成立;(3)求证:若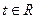 ,则不等式
,则不等式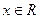 恒成立.
恒成立.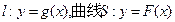 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件: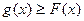 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.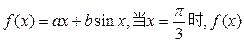 取得极小值
取得极小值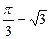 ,求a,b的值;
,求a,b的值;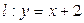 是(2)中曲线
是(2)中曲线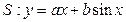 的“上夹线”。
的“上夹线”。
 有极值,求b的取值范围;
有极值,求b的取值范围; 处取得极值时,当
处取得极值时,当 恒成立,求c的取值范围;
恒成立,求c的取值范围; 都有
都有 .
.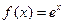 (
(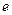 为自然对数的底数),
为自然对数的底数),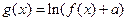 (
(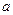 为常数),
为常数),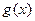 是实数集
是实数集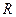 上的奇函数.(Ⅰ)求证:
上的奇函数.(Ⅰ)求证: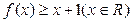 ;
;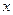 的方程:
的方程: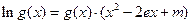
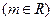 的根的个数;
的根的个数;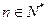 ,证明:
,证明: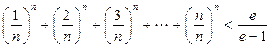 (
( ,函数
,函数 ,
, .
. 的单调区间和值域;
的单调区间和值域; 若
若 ,总存在
,总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.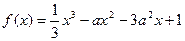 (a>0)
(a>0)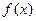 的单调区间,极大值,极小值
的单调区间,极大值,极小值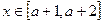 时,恒有
时,恒有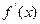 >
>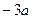 ,求实数a的取值范围
,求实数a的取值范围 x3 +
x3 +  ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.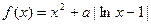 .(Ⅰ)当
.(Ⅰ)当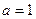 时,求曲线
时,求曲线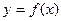 在
在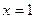 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当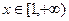 时,求函数
时,求函数 的最小值.
的最小值.