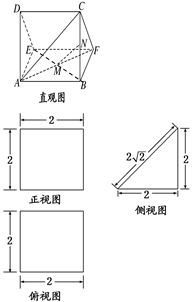
题目内容
在正方体 中,
中, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,则有
,则有
 中,
中, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,则有
,则有 A. | B. |
C. | D. |
A

连接
 ,因为
,因为 为正方体,所以
为正方体,所以 面
面 ,从而有
,从而有 ,所以
,所以 面
面 ,从而有
,从而有 ,所以
,所以 。
。连接
 ,因为
,因为 为正方体,所以
为正方体,所以 ,则
,则 是
是 与
与 所成角。因为
所成角。因为 ,所以
,所以 是等边三角形,从而可得
是等边三角形,从而可得 。
。因为
 为正方体,所以
为正方体,所以 ,则
,则 是
是 与
与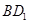 所成交。在
所成交。在 中可得
中可得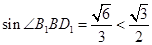 ,所以
,所以 ,从而有
,从而有 ,故选A
,故选A
练习册系列答案
相关题目

 中,
中, 是
是 的中点。
的中点。 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的余弦值.
的余弦值.
 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状; 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.
 中,
中, ,
, ,点
,点 在
在 上且
上且 (如图(3)).把
(如图(3)).把 沿
沿 向上折起到
向上折起到 的位置,使二面角
的位置,使二面角 的大小为
的大小为 (如图(4)).
(如图(4)). 的体积;
的体积; 与平面
与平面 所成角的正切值;
所成角的正切值; 为
为 上的点
上的点 ,使
,使 平面
平面
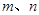 是两条不同的直线,
是两条不同的直线,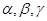 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: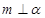 ,
,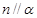 ,则
,则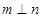 ②若
②若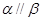 ,
,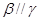 ,
,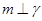
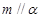 ,
,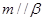 ,
,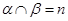 ,则
,则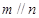 ④若
④若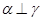 ,
,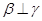 ,
,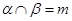 ,则
,则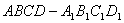 中,以顶点
中,以顶点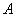 为端点的三条棱长都是
为端点的三条棱长都是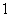 ,且它们彼此的夹角都是
,且它们彼此的夹角都是 ,则以
,则以



 、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上 .
、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上 .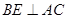 ;
;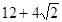 ;
;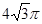 .
.