题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）经过点（ 
，1），且离心率为 
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设M、N是椭圆C上的点，直线OM与ON（O为坐标原点）的斜率之积为﹣ 
，若动点P满足 
，试探究，是否存在两个定点F1 ， F2 ， 使得|PF1|+|PF2|为定值？若存在，求F1 ， F2的坐标，若不存在，请说明理由．
【答案】解：（Ⅰ）∵椭圆C： 
=1（a＞b＞0）经过点（ 
，1），且离心率为 
，
∴ 
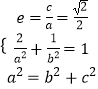，解得a=2，b= ，
∴椭圆C的方程为 
．
（Ⅱ）设P（x，y），M（x1 ， y1），N（x2 ， y2），
则由 
，得x=x1+2x2 ， y=y1+2y2 ，
∵M，N都在椭圆 上，
∴ 
，
∴ 
（ 
）
=（ 
）+4（ 
）+4（x1x2+2y1y2）
=20+4（x1x2+2y1y2），
设 
=﹣ 
，∴x1x2+2y1y2=0，
∴x2+2y2=20，∴点P是椭圆 
上的点，
∴由椭圆的定义知存在点F1 ， F2 ， 满足|PF1|+|PF2|=2 
=4 
为定值，
又∵|F1F2|=2 
=2 ，
∴F1 ， F2的坐标分别为F1（﹣ ，0），F2（ ，0）
【解析】（Ⅰ）由椭圆经过点（ ，1），且离心率为 ，列出方程组，求出a，b，由此能求出椭圆C的方程．（Ⅱ）由 ，得x=x1+2x2 ， y=y1+2y2 ， 由M，N都在椭圆 上，设 =﹣ ，得到点P是椭圆 上的点，由此能求出F1 ， F2的坐标．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
练习册系列答案
相关题目
