��Ŀ����
����Ŀ�����֮֮���敜���ҹ��ϱ���ʱ��ΰ��Ŀ�ѧ�ң�����ʵ���Ļ������������������ԭ���������Ƽ�ͬ����������족����˼�ǣ���������ȸߵļ�������ͬ�ߴ��صõĽ��������ȣ���ô������������������ȣ��˼��敜ԭ�����������ԭ����������ʱ����Ҫ����һ�����������ļ����壬��֪�ü���������ͼ��ͼ��ʾ����һ����ü�������µ���ƽ�����Ϊh��0��h��2����ƽ��ظü����壬��������Ϊ�� �� 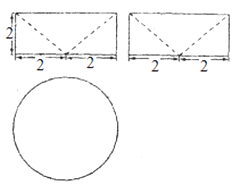
A.4��
B.��h2
C.��2��h��2
D.��4��h��2
���𰸡�B
���������⣺����֪�õ�������Ϊһ��Բ����ȥһ��Բ������뾶Ϊ2��Ϊ2��������Բ�뾶Ϊr���� ![]() ���õ�r=h�����Խ���Բ�����Ϊ��h2�� ��ѡB��
���õ�r=h�����Խ���Բ�����Ϊ��h2�� ��ѡB��
�����⣬���ȵõ�������Ϊһ��Բ����ȥһ��Բ���õ�����ΪԲ����ȷ��뾶�������

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����31���ļ�����ƥ���˶��Ὣ��2016��8��5�թ�21���ڰ�����Լ����¬���У��±��ǽ������˻��й������źͶ���˹�����Ż�õĽ�������ͳ�����ݣ���λ��ö����
��30���� | ��29�챱�� | ��28���ŵ� | ��27��Ϥ�� | ��26���������� | |
�й� | 38 | 51 | 32 | 28 | 16 |
����˹ | 24 | 23 | 27 | 32 | 26 |
�����ݱ���������������ɽ������˻����������Ż�õĽ������ľ�Ҷͼ����ͨ����Ҷͼ�Ƚ����������Ż�õĽ�������ƽ��ֵ����ɢ�̶ȣ���Ҫ������������ֵ���������ۼ��ɣ���
���ס��ҡ������˾��½����й������źͶ���˹�������е���һ����õĽ������ࣨ�������������Ż�õĽ�����������ȣ����涨�ס��ҡ���������������������ѡһ������֪�ס��Ҳ��й������ŵĸ��ʶ�Ϊ ![]() �������й������ŵĸ���Ϊ
�������й������ŵĸ���Ϊ ![]() �����˸��Բ��ĸ������ŵĽ������Ӱ�죮���üס��ҡ�������һ�Σ��������в��й������ŵ�����ΪX����X�ķֲ��м���ѧ����EX��
�����˸��Բ��ĸ������ŵĽ������Ӱ�죮���üס��ҡ�������һ�Σ��������в��й������ŵ�����ΪX����X�ķֲ��м���ѧ����EX��
