题目内容
已知数列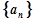 的前
的前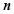 项和为
项和为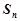 ,
,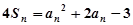 ,若
,若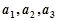 成等比数列,且
成等比数列,且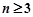 时,
时,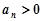 .
.
(1)求证:当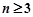 时,
时,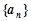 成等差数列;
成等差数列;
(2)求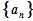 的前n项和
的前n项和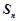 .
.
(1)见解析 (2)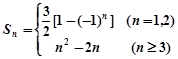
解析试题分析:
(1)该问已知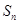 与
与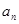 的一个关系,可以利用
的一个关系,可以利用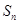 与
与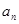 之间的关系(
之间的关系( )消
)消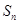 得到关于
得到关于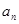 与
与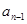 的二次等式,利用十字相乘法即可得到
的二次等式,利用十字相乘法即可得到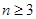 时,
时,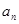 的相邻两项之差为常数,即为等差数列.
的相邻两项之差为常数,即为等差数列.
(2)分别令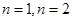 带入
带入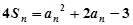 ,得到
,得到 的值,再利用第一问的结论可以求出
的值,再利用第一问的结论可以求出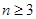 时,
时,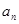 的通项公式,分
的通项公式,分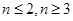 对
对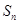 进行求解.
进行求解.
试题解析:
(1) 由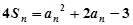 ,
, ,
,
得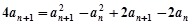 ,
,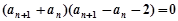 . 4分
. 4分
因为 ,
,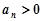 ,所以
,所以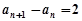 .
.
所以,当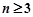 时,
时,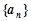 成等差数列. 7分
成等差数列. 7分
(2)由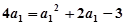 ,得
,得 或
或 .
.
又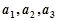 成等比数列,所以
成等比数列,所以 (
(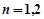 ),
),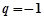 ,
,
而 ,所以
,所以 ,从而
,从而 .
.
所以 , 11分
, 11分
所以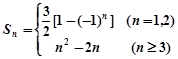 . 14分
. 14分
考点:等差数列 前n项和

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
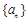 满足
满足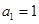 ,
,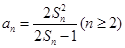 .
.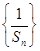 为等差数列;
为等差数列;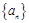 的通项公式;
的通项公式; 时,若
时,若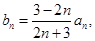 求
求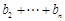 的值.
的值.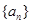 是公比大于
是公比大于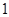 的等比数列,
的等比数列,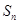 为数列
为数列 项和.已知
项和.已知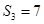 ,且
,且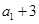 ,
,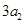 ,
,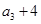 构成等差数列.
构成等差数列.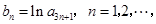 求数列
求数列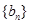 的前
的前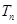 .
.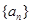 是公差不为0的等差数列,
是公差不为0的等差数列,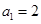 ,且
,且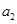 ,
,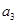 ,
, 成等比数列.
成等比数列.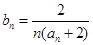 ,求数列
,求数列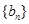 的前
的前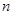 项和
项和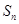 。
。 的前
的前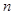 项和为
项和为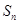 ,且
,且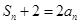 ,数列
,数列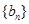 满足
满足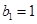 ,且
,且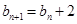 .
.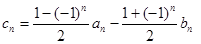 ,求数列
,求数列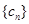 的前
的前 项和
项和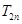 .
.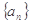 中,
中, 为常数,
为常数,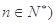 ,且
,且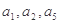 成公比不等于1的等比数列
成公比不等于1的等比数列 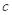 的值;
的值; ,求数列
,求数列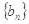 的前
的前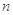 项和
项和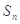
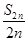 =2013,求n的值;
=2013,求n的值;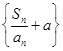 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+ .
.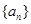 是等差数列,公差为
是等差数列,公差为 ,首项
,首项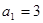 ,前
,前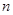 项和为
项和为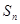 .令
.令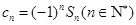 ,
,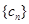 的前
的前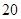 项和
项和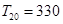 .数列
.数列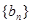 满足
满足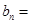
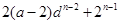 ,
,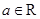 .
.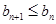 ,
,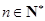 ,求
,求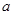 的取值范围.
的取值范围.