题目内容
已知数列 的前
的前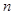 项和为
项和为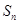 ,且
,且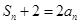 ,数列
,数列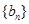 满足
满足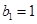 ,且
,且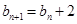 .
.
(1)求数列 ,
,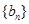 的通项公式;
的通项公式;
(2)设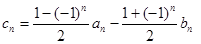 ,求数列
,求数列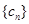 的前
的前 项和
项和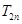 .
.
(1)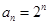 .
.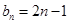 . (2)
. (2)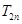
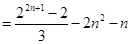 .
.
解析试题分析:(1)由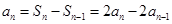 ,得
,得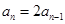 .
.
明确 是等比数列,公比为2,首项
是等比数列,公比为2,首项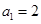 ,得到
,得到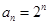 .
.
由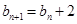 ,得
,得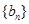 是等差数列,公差为2. 可得
是等差数列,公差为2. 可得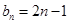 .
.
(2)由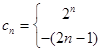
 利用“分组求和法”.
利用“分组求和法”.
试题解析:(1)当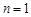 ,
,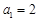 ; 1分
; 1分
当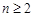 时,
时,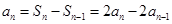 ,∴
,∴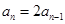 . 2分
. 2分
∴ 是等比数列,公比为2,首项
是等比数列,公比为2,首项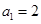 , ∴
, ∴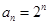 . 3分
. 3分
由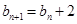 ,得
,得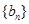 是等差数列,公差为2. 4分
是等差数列,公差为2. 4分
又首项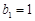 ,∴
,∴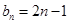 . 6分
. 6分
(2)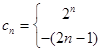
 8分
8分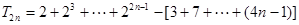 10分
10分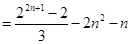 . 12分
. 12分
考点:等差数列、等比数列的通项公式及其求和公式,“分组求和法”.

练习册系列答案
相关题目
 是首项为
是首项为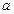 ,公差为
,公差为 的等差数列(d≠0),
的等差数列(d≠0),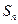 是其前
是其前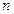 项和.记bn=
项和.记bn= ,
,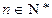 ,其中
,其中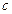 为实数.
为实数.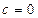 ,且
,且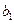 ,
, ,
, 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+); 是等差数列,证明:
是等差数列,证明: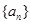 的前
的前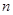 项和
项和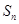 满足
满足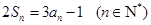 ,等差数列
,等差数列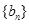 满足
满足 .
.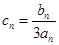 ,求数列
,求数列 的前
的前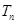 .
.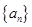 是等差数列,且
是等差数列,且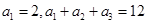 .
.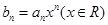 ,求数列
,求数列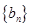 的前
的前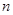 项和.
项和. ,数列
,数列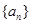 满足
满足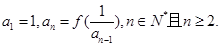
 ,设
,设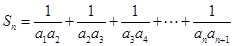 ,若
,若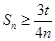 恒成立,求实数
恒成立,求实数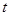 的取值范围.
的取值范围.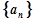 的前
的前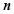 项和为
项和为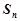 ,
,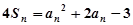 ,若
,若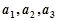 成等比数列,且
成等比数列,且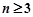 时,
时,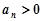 .
.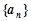 成等差数列;
成等差数列;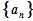 的前n项和
的前n项和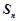 .
.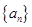 是公比为
是公比为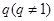 的等比数列,且
的等比数列,且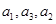 成等差数列.
成等差数列.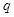 的值;
的值;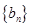 是以
是以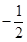 为首项,
为首项,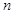 项和
项和 .
.